The circle centered at origin is inscribed in the parabola . Which of the following is/are true?
Radius of circle is sqrt
Radius of circle is
Common tangent to circle and parabola passes from
Length of common chord for circle and parabola is
The correct Answer is:A, C
Equation of circle is
To find points of intersection A&B
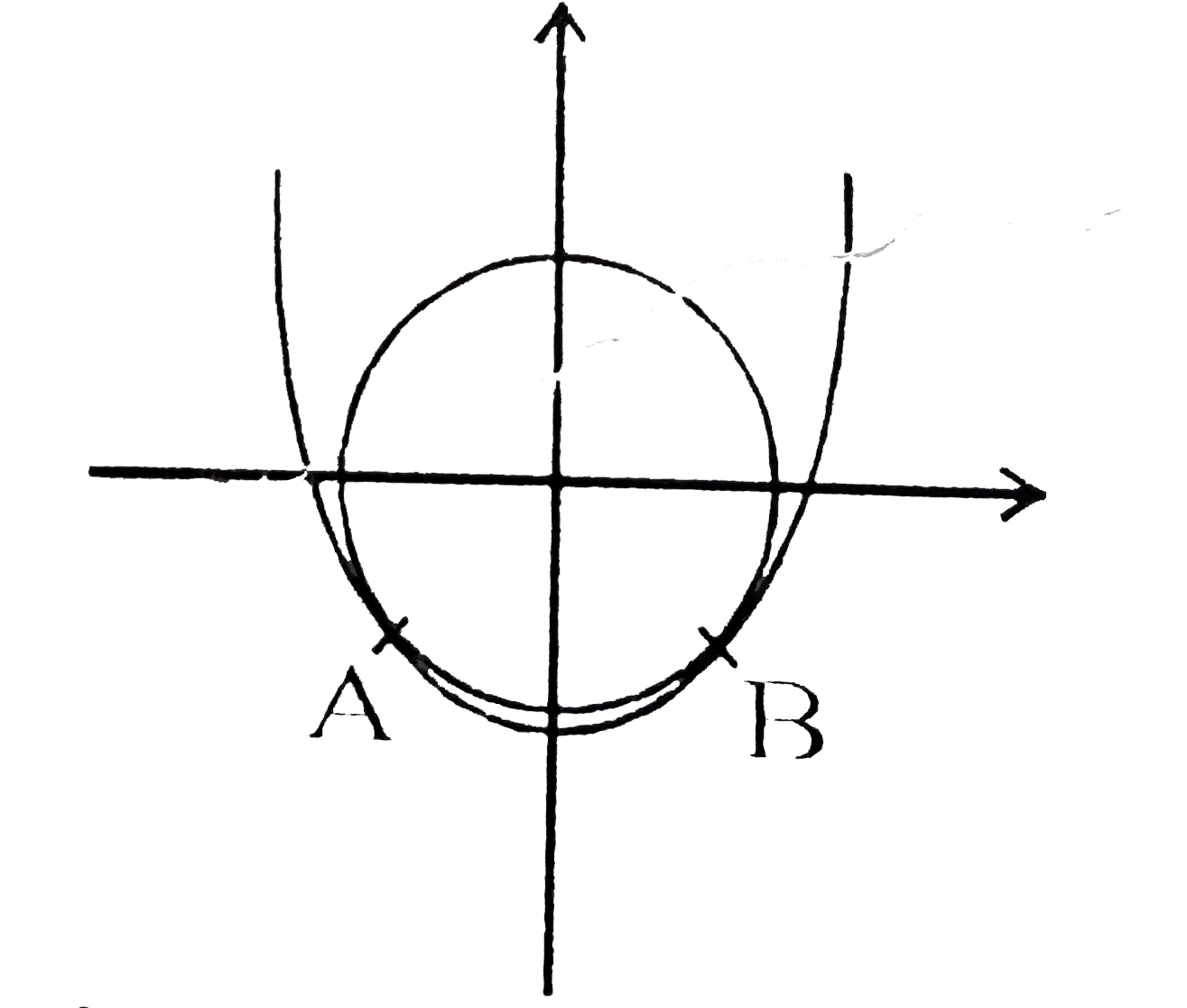
Tangent at
at
Length
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - part-2 Mathematics
48 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PHYSICS
140 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - part-2 Mathematics
15 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - CHEMISTRY SECTION-II
16 Videos
- VECTOR ALGEBRABOOK - ALLEN CHAPTER - VECTOR ALGEBRAEXERCISE - All Questions
1 Videos
Similar Questions
Knowledge Check
Consider the circle x2+y2–2x–2y–14=0, which of following is/are true :
APoint (3, 4) lies insides the circleBPoint (–5, –3) lies outside the circleCLine x + 3y + 4 = 0 is diameter of circleDArea of circle is 16π square unitsFor the circle x2+y2+3x+3y=0, which of the following relation is true ?
ACentre lies on X-axisBCentre lies on Y-axisCCentre is at originDCircle passes through originFor the circle x2+y2+6x−8y+9=0, which of the following statement is true ?
ACircle passes through the point (−3,4)BCircle touches X-axisCCircle touches Y-axisDNone of these
An Equilateral triangle is inscribed in the parabola y^(2)=4x if one vertex of triangle is at the vertex of parabola then Radius of circum circle of triangle is
View SolutionIf an equilateral triangle is inscribed in a parabola y2=12x with one of the vertices being at the vertex of the parabola then its height
View SolutionIf an equilateral triangle is inscribed in a parabola y2=12x with one of the vertices being at the vertex of the parabola then its height is
View SolutionAn equilateral triangle is inscribed in the parabola y2=8x with one of its vertices is the vertex of the parabola. Then, the length or the side or that triangle is
View SolutionIn the figure, ΔABC is inscribed in the circle. The triangle does not contain the center of the circle O. Which one of the following could be the value of x in degree?
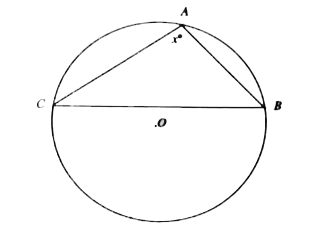
View Solution
