Force acting on a particale is (2ˆi+3ˆj)N. Work done by this force is zero, when the particle is moved on the line 3y+kx=5. Here value of k is (Work done W=→F.→d)Solution in Gujrati
2
4
6
8
The correct Answer is:A
Displacement d→r=dxˆi+dyˆj
but 3y+kx=5 so 3dy+kdx=0
⇒d→r=dxˆi−k3dxˆj=(ˆi−k3ˆj)dx
Work done is zero if →F.d→r=0
(2ˆi+3ˆj).(ˆi−k3ˆj)dx=0⇒(2−k)dx=0⇒k=2
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-03
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-04
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exersice -05(B)
20 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
Two parallel metallic plates have surface charge densities σ1 and σ2 as shown in figure.
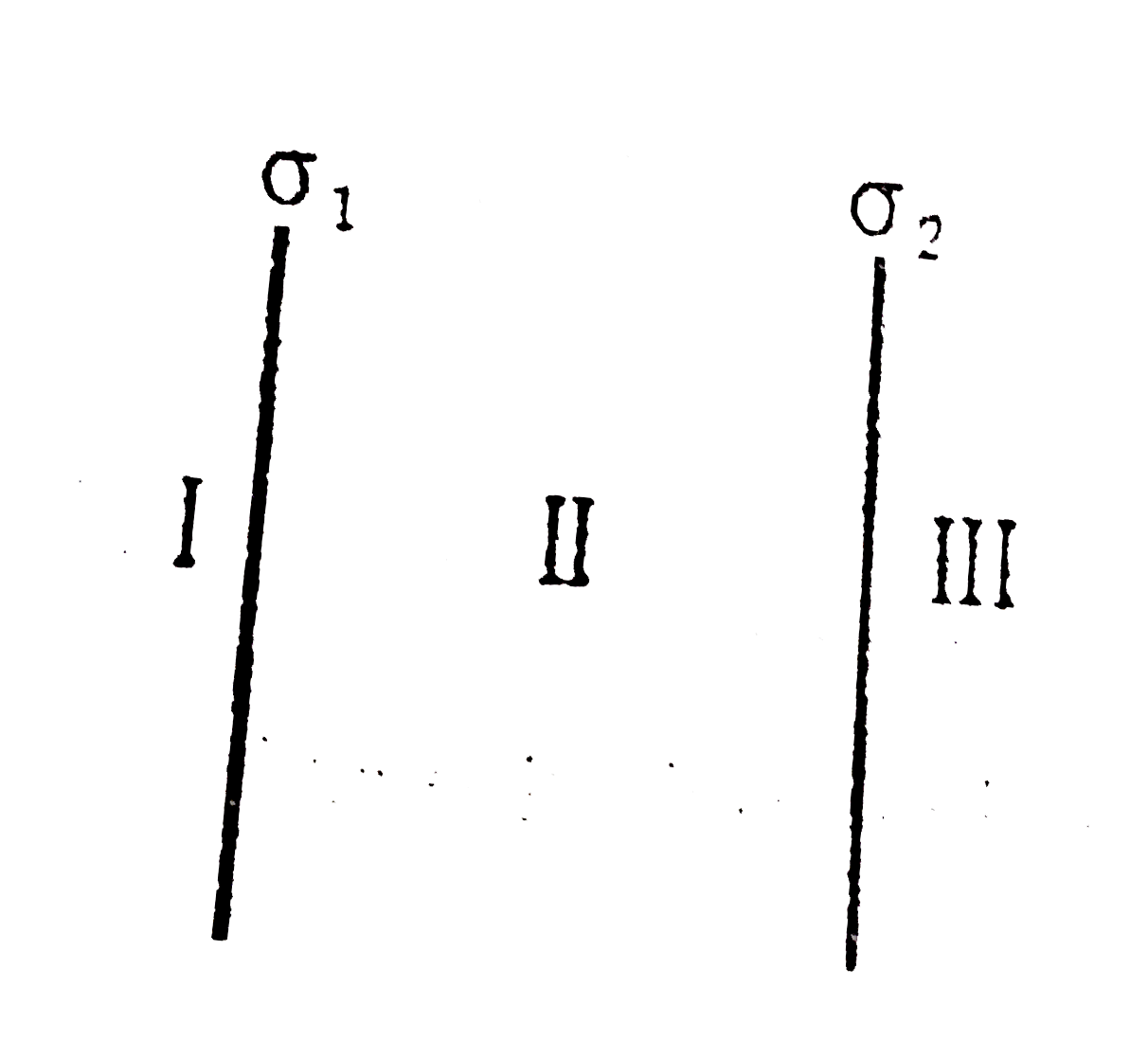
Column-IColumn-II(A)If σ1+σ2=0(p)Electric field in region III is towards right(B)Ifσ1+σ2>0(q)Electric field in region I is zero(C)If σ1+σ2<0(r)Electric field in region I is towards roght(s)Nothing can be said
View SolutionIn each situation of Column-I two elelctric dipoles having moments →p1 and →p1 of same magnitude (that is ,p1=p2) are placed on x-axis symmetrically about origin in different orientations as shown. In column-II certain inferences are drawn for these two dipoles. Then match the different orientations of dipole in column-I with the corresponding result in column-II.

View SolutionPlanck's constant has dimensions …………….
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionForce acting on a particle is )jˆ3 iˆ (2 N. Work done by this force is zero. when a particle is moved on the line 3y + kx = 5. Here value of k is:

View SolutionForce acting on a particale is (2hat(i)+3hat(j))N . Work done by this force is zero, when the particle is moved on the line 3y+kx=5 . Here value of k is ( Work done W=vec(F).vec(d))
View SolutionA force →F=3ˆi+cˆj+2ˆk acting on a particle causes a displacement →d=−4ˆi+2ˆj+3ˆk. If the work done is 6j. Find the value of 'c' ?
View SolutionA force →F=3ˆi+cˆj+2ˆk acting on a particle causes a displacement →d=−4ˆi+2ˆj+3ˆk. If the work done is 6J then the value of 'c' is
View SolutionFind the work done in moving a particle along a vectors →S=(ˆi−2ˆj+3ˆk)m if applied force is →F=(2ˆi−3ˆj+4ˆk)N.
View SolutionA force vec(F)=2hat(i)-3hat(j)+7hat(k) (N) acts on a particle which undergoes a displacement vec(r )=7hat(j)+3hat(j)-2hat(k)(m) . Calculate the work done by the force.
View SolutionForce acting on a particle is (2hati+3hatj) N. Work done by this force is zero ,when a particle is moved on the line 3y+kx=5 . Here value of k is
View SolutionForce acting on a particle is (2hati+3hatj)N . Work done by the force is zero, when a particle is moved along the line 3y+kx=5 . Here the value of k is
View SolutionForce acting on a particle is (2ˆi+3ˆj)N. Work done by the force is zero, when a particle is moved along the line 3y+kx=5. Here the value of k is
View SolutionForce acting on a particle is (2ˆi+3ˆj)N. Work done by the force is zero, when a particle is moved along the line 3y+kx=5. Here the value of k is
View SolutionIf vec(F) = 3hat(i) + 4hat(j) + 5hat(k) and vec(S) = 6hat(i) + 2hat(j) + 5hat(k) , find the work done by the force.
View Solution
