In a uniform electric field, the potential is 10V at the origin of coordinates , and 8V at each of the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). The potential at the point (1, 1,1 ) will be .Solution in Gujrati
0
4V
8V
10V
The correct Answer is:B
Here potential decreases 2V as we moves unit distance. Hence for point (1, 1, 1) from (0, 0, 0). The total potential decrease is 2+2+2=6V. Hence the potential at poinr will (10−6)=4V
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-03
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-04
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exersice -05(B)
20 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
Two parallel metallic plates have surface charge densities σ1 and σ2 as shown in figure.
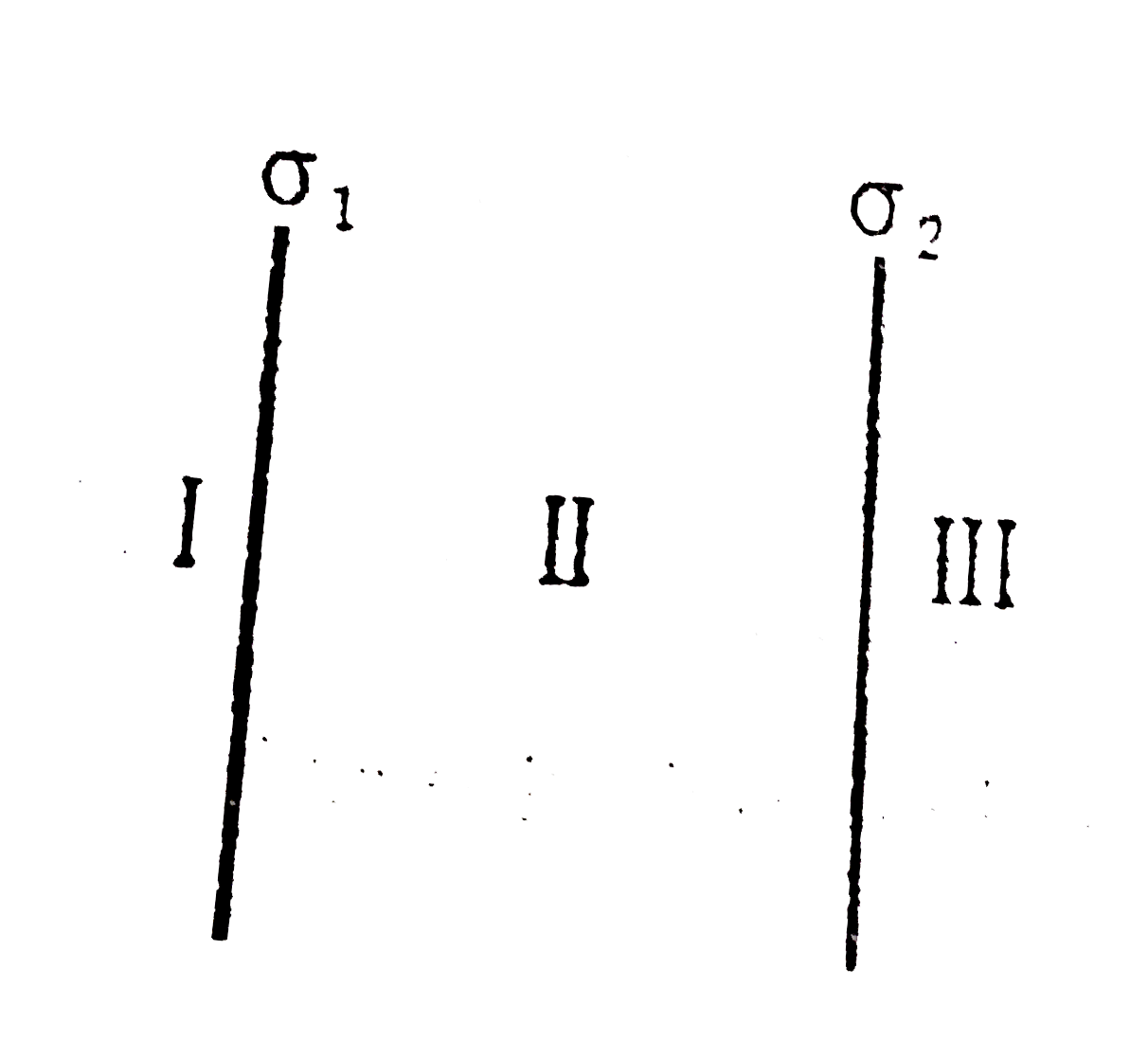
Column-IColumn-II(A)If σ1+σ2=0(p)Electric field in region III is towards right(B)Ifσ1+σ2>0(q)Electric field in region I is zero(C)If σ1+σ2<0(r)Electric field in region I is towards roght(s)Nothing can be said
View SolutionIn each situation of Column-I two elelctric dipoles having moments →p1 and →p1 of same magnitude (that is ,p1=p2) are placed on x-axis symmetrically about origin in different orientations as shown. In column-II certain inferences are drawn for these two dipoles. Then match the different orientations of dipole in column-I with the corresponding result in column-II.

View SolutionPlanck's constant has dimensions …………….
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionIf points (a, 0), (0, b) and (1, 1) are collinear, then 1a+1b= (a) 1 (b) 2 (c) 0 (d) −1
View SolutionIn a uniform electric fieled, the potential is 10V at the origin of coordinates , and 8 V at each of the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). The potential at the point (1, 1,1 ) will be .
View SolutionThe electric potential decreases uniformly from V to -V along X-axis in a coordinate system as we moves from a point (−x0,0) to (x0,0), then the electric field at the origin:
View SolutionThe grid represents a region in space containing a uniform electric field (each square of size 1m xx 1m ). If potentials at point O, A, B, C, D, E, F, G, H are respectively 0, -1, -2, 1, 2, 0, -1, 1 and 0 volts find the electric field intensity.
View SolutionThe x-coordinate of the incentre of the triangle that has the coordinates of mid points of its sides as (0, 1), (1, 1) and (1, 0) is
View SolutionIn an arrangement four particles, each of mass 2 gram are situated at the coordinate points (3, 2, 0), (1, –1, 0), (0, 0, 0) and (–1, 1, 0). The moment of inertia of this arrangement about the Z-axis will be
View SolutionTwo point charges-q and +q are located at points (0, 0,-a) and (0, 0, a) respectively. The electric potential at a point (0, 0, z), where z> a is
View SolutionElectric field in a region is given by E=(2hati+3hatj-4hatk)V//m . Find the potential difference between points (0, 0, 0) and (1,2,3) in this region.
View Solutionபுள்ளிகள் (1, 0, 0), (0, 1, 0) மற்றும் (0, 0, 1) ஆகியவற்றை முனைப் புள்ளிகளாகக் கொண்ட முக்கோணத்தின் நடுக்கோடுகளின் திசைக் கொசைன்களைக் காண்க.
View SolutionThe x-coordinate of the incentre of the triangle that has the coordinates of mid points of its sides as (0, 1), (1, 1) and (1, 0) is
View Solution
