Two ships, V and W, move with constant velocities 2ms−1 and 4ms−1 along two mutually perpendicular straight tracks toward the intersection point O. At the moment t=0, the ships V & W were located at distances 100m and 200m respectively from the point O.
The distance between them will be shortest at t= ........Solution in Gujrati
50 sec
10 sec
100 sec
None of these
The correct Answer is:A
For shortest distance dldt=0⇒t=50sec
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Comprehension 3
5 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Comprehension 4
6 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Comprehension 1
5 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
Path traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
The position vector of car w.r.t. its starting point is given as →r=atˆi−bt2ˆj where a and b are positive constants. The locus of a particle is:-
View SolutionIn a certain system of absolute units the acceleration produced by gravity in a body falling freely is denoted by 3, the kinetic energy of a 272.1kg shot moving with velocity 448 metres per second is denoted by 100, and its momentum by 10.
The unit of length is
View SolutionThe van der waal's gas equation is (P+aV2)(V−b)=RT, where P is pressure, V is molar volume and T is the temperature of the given sample of gas. R is called molar gas constant, a and b are called van der waal's constants.
The dimensional formula for b is same as that for
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionRam Shyam are walking on two perpendicular tracks with speed 3ms^(-1) and 4 ms^(-1) , respectively. At a certain moment (say t = 0s) , Ram and Shyam are at 20 m and 40 m away from the intersection of tracks, respectively, and moving towards the intersection of the tracks. During the motion the magnitude of velocity of ram with respect to Shyam is
View SolutionRam Shyam are walking on two perpendicular tracks with speed 3ms^(-1) and 4 ms^(-1) , respectively. At a certain moment (say t = 0s), Ram and Shyam are at 20 m and 40 m away from the intersection of tracks, respectively, and moving towards the intersection of the tracks. Shortest distance between them subsequently is
View SolutionRam Shyam are walking on two perpendicular tracks with speed 3ms^(-1) and 4 ms^(-1) , respectively. At a certain moment (say t = 0s), Ram and Shyam are at 20 m and 40 m away from the intersection of tracks, respectively, and moving towards the intersection of the tracks. The time t when they are at shortest distance from each other subsequently is -
View SolutionTwo cars (A) and (B) are at positions 100 m and 200 m from the origin at time t=0 . They start simultaneously with velocities 10 ms^(-1) respectively. The car (A) will overtake the car (B) at a distance of .
View SolutionTwo particles, 1 and 2, move with constant velocities v_1 and v_2 along two mutually perpendicular straight lines toward the intersection point O. At the moment t=0 the particles were located at the distances l_1 and l_2 from the point O. How soon will the distance between the particles become the smallest? What is it equal to?
View SolutionTwo particles move with constant velocities towards point O along straight lines in a plane as shown. The shortest distance A and B is

View SolutionTwo ships, 1 and 2, move with constant velocities 3 m/s and 4 m/s along two mutually perpendicular straight tracks toward the intersection point O. At the moment t = 0 the ships were located at the distances 120 m and 200 m from the point O. How soon will the distance between the ships become the shortest and what is it equal to ?
View SolutionTwo particles A and B move with constant velocities v_(1) and v_(2) along two mutually perpendicular strainght lines. Towards the intersection point O. At moment t = 0 the particle were located at distance l_(1) and l_(2) from O respectively. Find the time when they are nearest and also this shortest distance
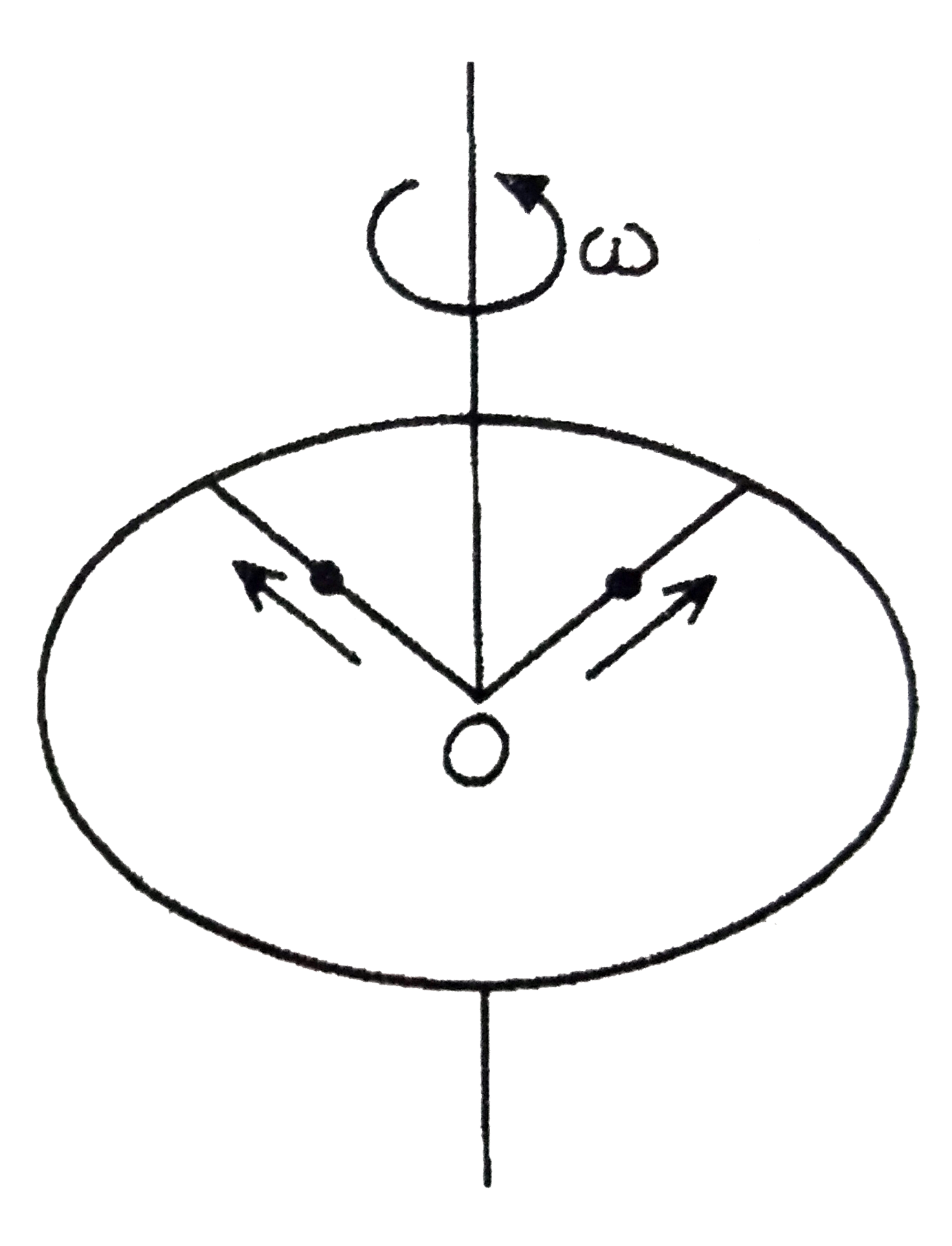
View Solutionद्रव्यमान M तथा त्रिज्या R का एक छल्ला अपने केंद्र से होकर जाने वाली स्थिर ऊर्ध्वाधर अक्ष के परितः कोणीय वेग ω से घूम रहा है। इस क्षण M/8 द्रव्यमान के दो बिंदु द्रव्यमान छल्ले के केंद्र O पर विराम स्थिति में है। वो दर्शाये चित्रानुसार छल्ले पर लगी द्रव्यमानहीन दो छड़ों पर त्रिज्यतः बाहर की ओर गति कर सकतेक हैं किसी क्षण पर निकाय की कोणीय गति 89ω है तथा बिंदु द्रव्यमान O से 35R दूरी पर है। इस क्षण दूसरे बिंदु द्रव्यमान की O से दूरी होगी:
View Solutionएक कण सरल रेखा में नियत त्वरण से गति कर रहा है। t सेकण्ड में 135 m दूरी तय करने के बाद इसका वेग 10ms−1 से 20ms−1 हो जाता है। तब t का मान है
View SolutionTwo particles A and B move with constant velocities v1 and v2 along two mutually perpendicular straight lines towards the intersection point O.At moment t=0,the particle were located at distancce l1 and l2 from O. respectively .Find the time,when they are nearest and also the shortest distance between them.
View Solution
