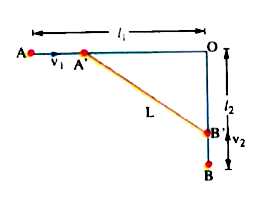
Two particles A and B move with constant velocities v1and v2along two mutually perpendicular straight lines towards the intersection point O. At moment t=0, the particle were located at distance 11and12from O, respectively. Find the eime , when they are nearest and also the shortest distance between them .
After time .t. , the position of the point
A and B are(191)−v1t)and(12−v2t),respectively
The distance L between the points A.andB. are
L2=(11−v1t)2+(12−v2t)2
Differentiating with restect to time,
2LdLdt=2(11−v1t)(−v1)+2(12−v2t)(−v2)
From minimum value of LdLdt=0
putting the value of t in equation (1)
Lmin=|11v2_+12v1|√v21+v22
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Very Short Answer Type Questions
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE (LEVEL 1)
22 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise -3
31 Videos
- MOTION IN A PLANE BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANE EXERCISE - Practice Exercise
84 Videos
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANECED) (Matrix Matching Type Questions)
1 Videos
Similar Questions
Two particles A and B move with constant velocities v1 and v2 along two mutually perpendicular strainght lines. Towards the intersection point O. At moment t=0 the particle were located at distance l1 and l2 from O respectively. Find the time when they are nearest and also this shortest distance
View SolutionTwo particles, 1 and 2, move with constant velocities v1 and v2 along two mutually perpendicular straight lines toward the intersection point O. At the moment t=0 the particles were located at the distances l1 and l2 from the point O. How soon will the distance between the particles become the smallest? What is it equal to?
View Solution
Knowledge Check
Two ships, V and W, move with constant velocities 2ms−1 and 4ms−1 along two mutually perpendicular straight tracks toward the intersection point O. At the moment t=0, the ships V & W were located at distances 100m and 200m respectively from the point O.
The distance between them at time t is :-Aa2y+bx2=0Ba2y=bx2Cy=ba2xDay2=b2xTwo ships, V and W, move with constant velocities 2ms−1 and 4ms−1 along two mutually perpendicular straight tracks toward the intersection point O. At the moment t=0, the ships V & W were located at distances 100m and 200m respectively from the point O.
The distance between them will be shortest at t= ........A2bˆjBaˆjC(a−2b)ˆiDNone of theseTwo particles move with constant velocities towards point O along straight lines in a plane as shown. The shortest distance A and B is
 A50√3cmB300cmC100√3cmD200cm
A50√3cmB300cmC100√3cmD200cm
Two particles, 1 and 2, move with constant velocities v1 and v2 along two mutually perpendicular straight lines toward the intersection point O. At the moment t=0 the particles were located at the distances l1 and l2 from the point O. How soon will the distance between the particles become the smallest? What is it equal to?
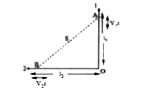
View SolutionTwo particles A and B move with constant velocity →v1 and →v2 along two mutually perpendicular straight lines towards intersection point O as shown in figure, At moment t = 0 particles were located at distance l1 and l2 respectively from O. Then minimu distance between the particles and time taken are respectively
View SolutionTwo ships, V and W, move with constant velocities 2ms−1 and 4ms−1 along two mutually perpendicular straight tracks toward the intersection point O. At the moment t=0, the ships V & W were located at distances 100m and 200m respectively from the point O.
The distance between them will be shortest at t= ........
View SolutionTwo ships, V and W, move with constant velocities 2ms−1 and 4ms−1 along two mutually perpendicular straight tracks toward the intersection point O. At the moment t=0, the ships V & W were located at distances 100m and 200m respectively from the point O.
The distance between them will be shortest at t= ........
View SolutionTwo ships, 1 and 2, move with constant velocities 3 m/s and 4 m/s along two mutually perpendicular straight tracks toward the intersection point O. At the moment t=0 the ships were located at the distances 120 m and 200 m from the point O. How soon will the distance between the ships become the shortest and what is it equal to ?
View Solution
