The diagram show a small bead of mass m carrying charge q. The bead can freely move on the smooth fixed ring placed on a smooth horizontal plane . In the same pane a charge +Q has also been fixed as shown. The potential at the point P due to +Q is V . The velocity which the bead should projected from the point P so that it can complete a circle should be greater than .
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:A
Given VA due to +Q is V, so VB=4V
By energy conservation
12mu2+qV=4qV
⇒u=√6qVm

Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-03
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-04
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exersice -05(B)
20 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
Two parallel metallic plates have surface charge densities σ1 and σ2 as shown in figure.
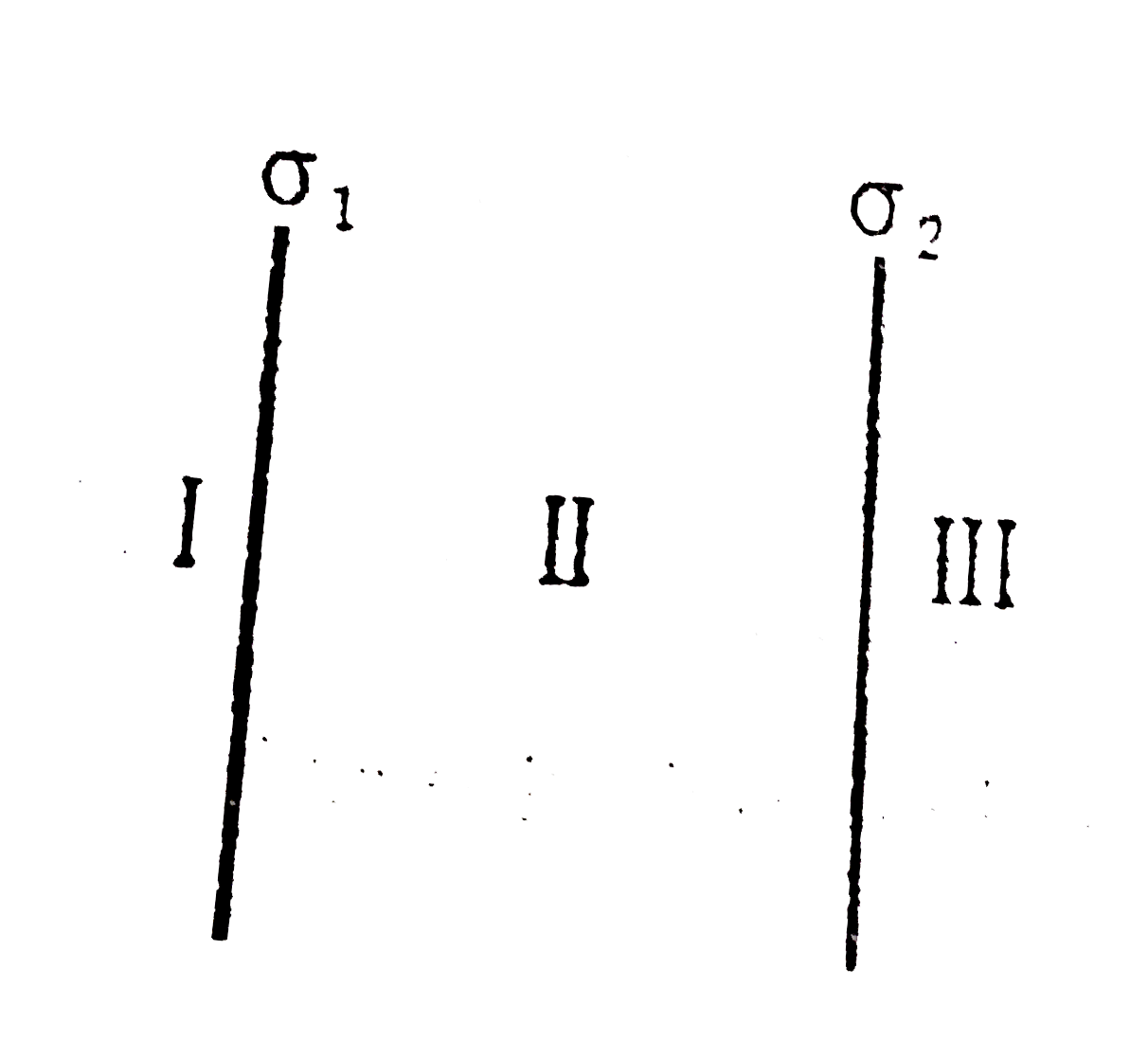
Column-IColumn-II(A)If σ1+σ2=0(p)Electric field in region III is towards right(B)Ifσ1+σ2>0(q)Electric field in region I is zero(C)If σ1+σ2<0(r)Electric field in region I is towards roght(s)Nothing can be said
View SolutionIn each situation of Column-I two elelctric dipoles having moments →p1 and →p1 of same magnitude (that is ,p1=p2) are placed on x-axis symmetrically about origin in different orientations as shown. In column-II certain inferences are drawn for these two dipoles. Then match the different orientations of dipole in column-I with the corresponding result in column-II.

View SolutionPlanck's constant has dimensions …………….
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
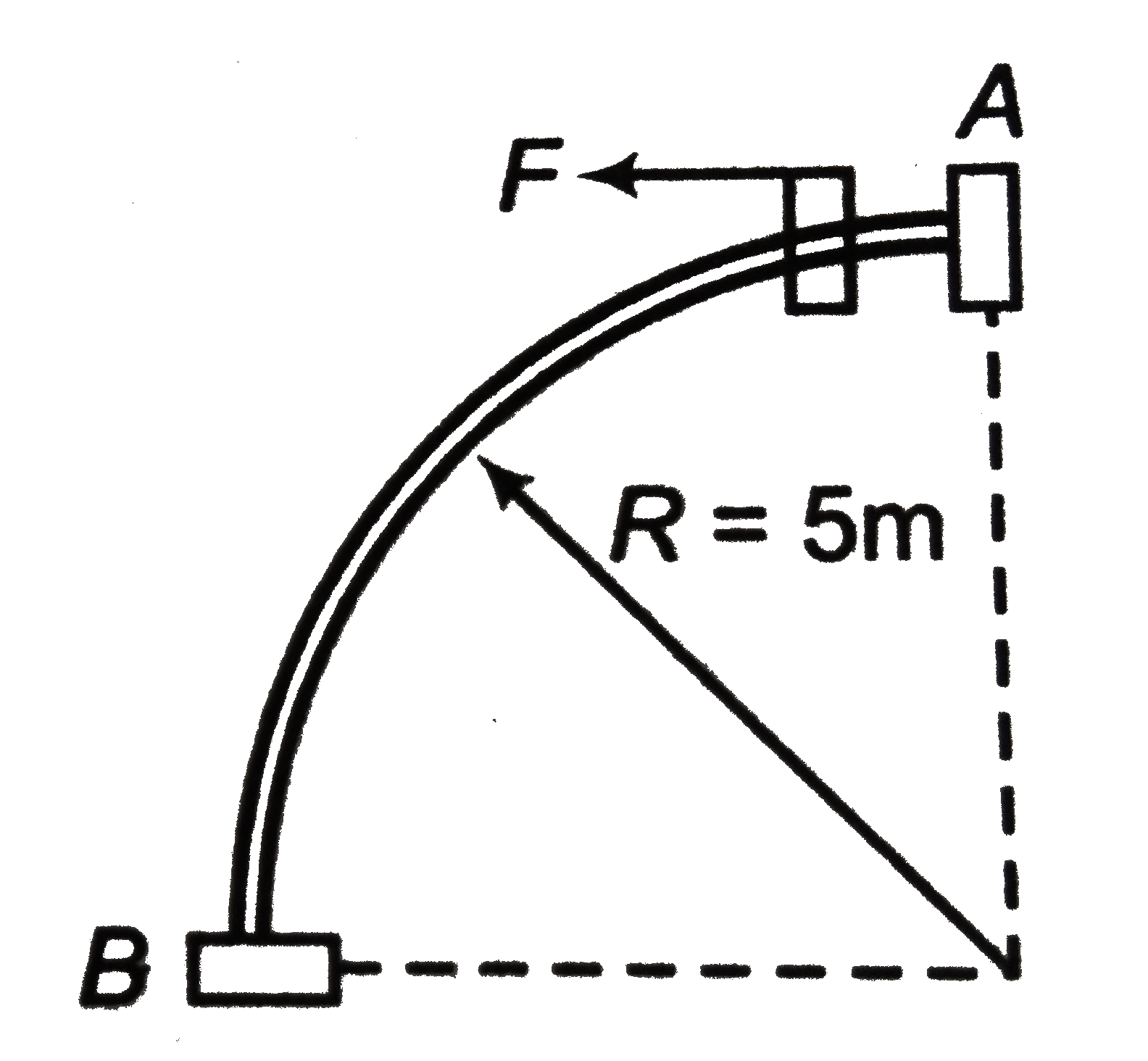
View SolutionA bead of mass 12kg starts from rest from A to move in a vertical place along a smooth fixed quarter ring of radius 5m, under the action of a constant horizontal force f=5N as shown. The speed of bead as it reaches the point (B) is [Take g=10ms−2]
View SolutionTwo small beads having positive charges 3q and q are fixed at the opposite ends of a horizontal, insulating rod, extending from the origein to the point x=d as shown in fig. A third small charged bead is free to slide on the rod. At what position is the third bead in equilibrium? Can it be in stable eqyilibrium ?
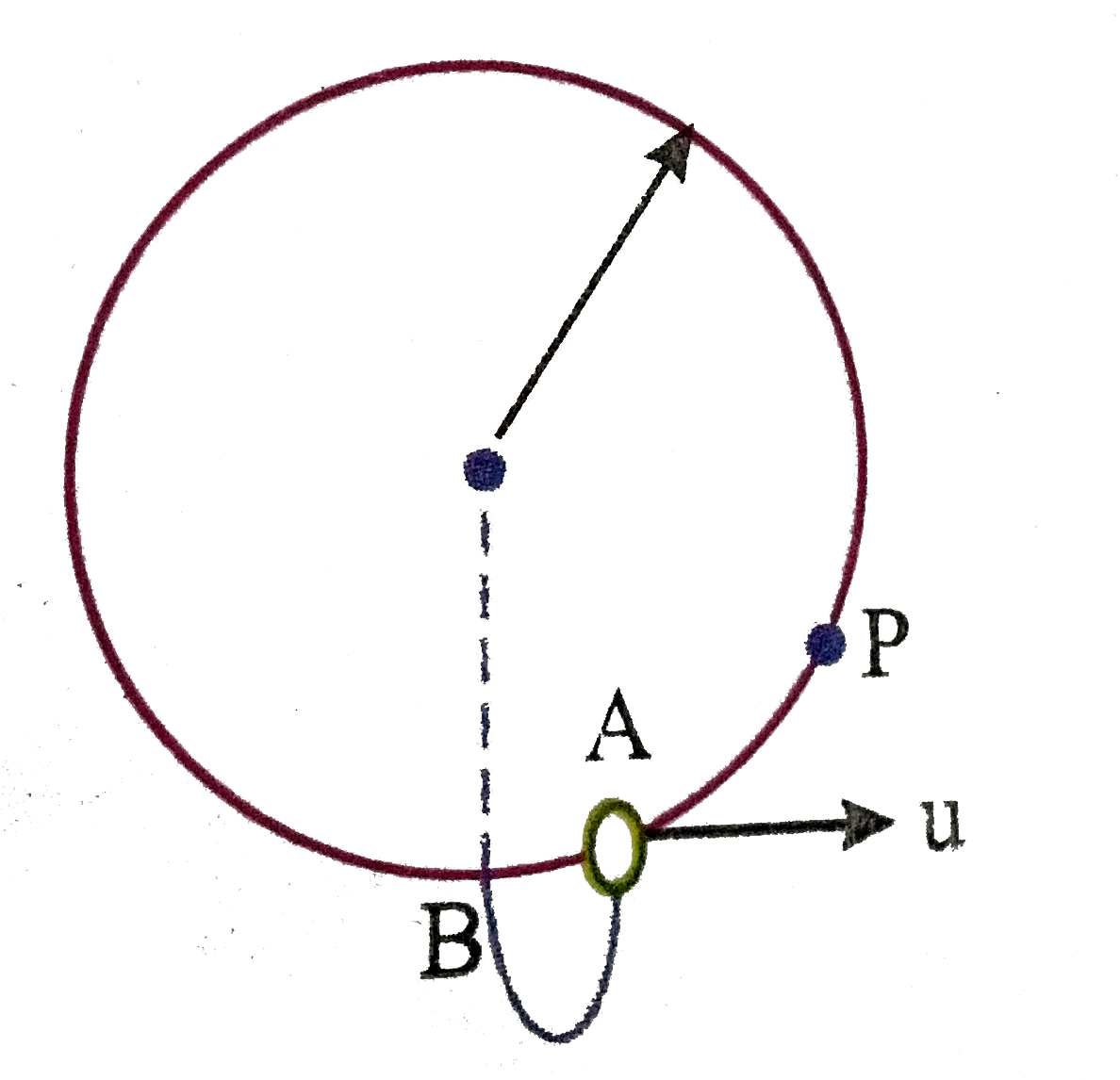
View SolutionThe diagram show a small bead of mass m carrying charge q. The bead can freely move on the smooth fixed ring placed on a smooth borizontal plane . In the same pane a charge +Q has also been fixed as shown. The potential at the point P due to +Q is V . The velocity which the bead should projected from the point P so that it can complete a circle should be greater than .

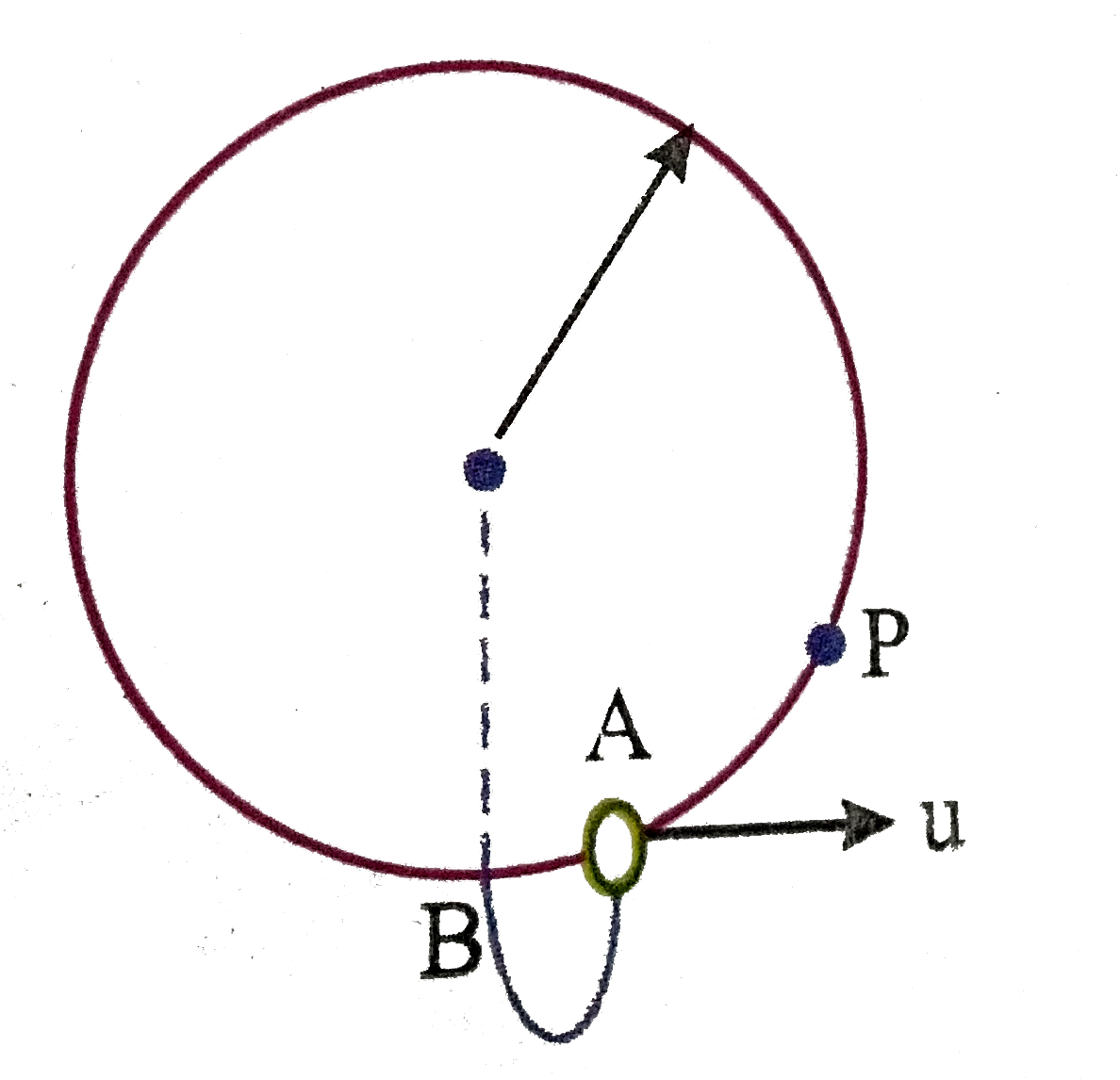
View SolutionA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.
The smallest value u0 of u for which the bead will make complete revolutions of the wire will be
View SolutionA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.

If v=2u0, the tension T in th elastic string when the bead is at the highest point B of the wire is
View SolutionA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.
The elastic energy stored in the string when the bead is at the highest point B will be
View SolutionA bead is connected with a fixed disc of radius R by an inextensible massless string in a smooth horizontal plane. If the bead is pushed with a velocity v_(0) prependicular to the string, the bead moves in a curve and consequently collapses on the disc. Then
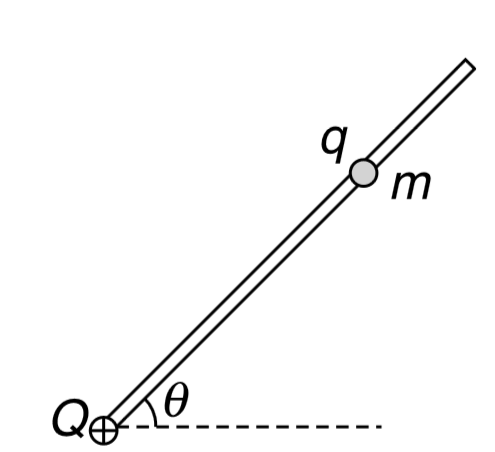
View SolutionA smooth fixed rod is inclined at an angle θ to the horizontal. At the bottom end of the rod there is a fixed charge +Q. There is a bead of mas m having charge q that can slide freely on the rod. The equilibrium separation of the bead from fixed charge Q is x0 Find the frequency of oscillation of the bead if it is displaced a little from its equilibrium position.
View SolutionA small bead of mass m can moves on a smooth circular wire (radiusR) under the action of a force F=kmr2 directed (r=position of bead from P&K=constant) towards a point P with in the circle at a distance R2 from the centre what should be the minimum velocity of bead at the point of the wire nearest the centre of force (P) so that bead will complete the circle

View SolutionA bead of mass "m" and charge "q" is threaded on a smooth wire kept along "x" -axis. A second charge "Q" is fixed at the point "x=0" ,"y=-d." It is projected with high speed so that it is initially near "x=-infinity" and it ends up near "x=+infinity." As the moving charge passes thebstationary charge, find the impulse exerted by the wire on the bead. Neglect gravity and assume the speed to be constant.
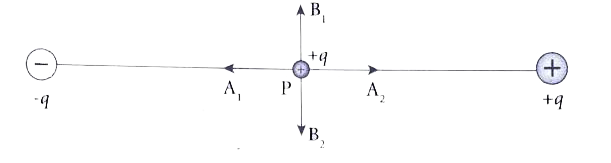
View SolutionTwo identical point charges'of magnitude -q are fixed as shown in the figure below. A third charge +q is placed midway between the two charges at the point P. Suppose this charge is displaced a small distance from the point P in the directions indicated by the arrows, in which direction(s) will +q be stable with respect to the displacement?
View Solution
