The method of electrical images is used to solve the electrostatic problems, where charge distribution is not specified completely. The method consists of replacement of given charge distribution by a simplified charge distribution or a signal point charge or a number of point charges [rovided the original boundary conditions are still satisfied. For example consider a system consider a system containing a point charge q placed at a distance d of form an infinite conducting plane. The boundary conditions are :
(i) Potential is zero at infinity (ii) Potential is zero at each point on the conducting plane If we replaced the conducting plane by a point charge (-q) placed at a distance 'd' opposite to conducting plane. The charge (-q) is called the electrical image.
Now system consists of two charge +q an -q at seperation2d. If charge +q moves to a distance 'y' from the boundary of conducting plane (now absent), the electrical image -q also moves to the same 'y' from the boundary of conducting plane, so that the new distance between +q and -q is 2y

The potential energy of system of charge +q placed at a distance d from the earthed conducting plane isSolution in Gujrati
14π∈0q2d2
−14π∈0q22d2
14π∈0q22d
−14π∈0q24d
The correct Answer is:D
Potential energy=−∫→F.d→r
=+d∫∞q24π∈0(2r)2dr=−14π∈0q24d
Note : Here potential energy ≠−14π∈0q22d because it is not an electrostatic field.
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Comprehension 8
4 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Comprehension 9
2 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Comprehension 6
3 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
In previous question if the particles started from rest and all are positively charge which particles must have been acted upon by a force other than that produced by the electric field.
View SolutionFlow cytometry, illustrated in the figure, is a technique used to sort cells by type. The cells are placed in a conducting saline solution which is then forced from a nozzle. The stream breaks up into small droplets, each containing one cell. A metal collar surrounds the stream right at the point where the droplets seprate from the stream. Charging the collar polarizes the conducting liquid, causing the droplets to become charged as they break off from the steam. A leser beam probes the solution just upstream from the charging collar, looking for the presence of certain types of cells. All droplets containing one particular type of cell are given the same charge by the charging collar. Droplets with other desired types of cells receive a different charge, and droplats with no desired cell receive no charge. The charged. The charges droplets then pass between two parallel charged electrodes where they receive a horizontal force that directs force that directs them into different collection tubes, depending on air charge.

View SolutionThe sketch below show cross section so equipotential surfaces between two charged.Conductors that are shown in solid black.Some points on the equipotenital surfaces .near the conductors are marked as A,B,C….. The arrangements lies in air (Take ε0=8.85×10−12C2/Nm2]
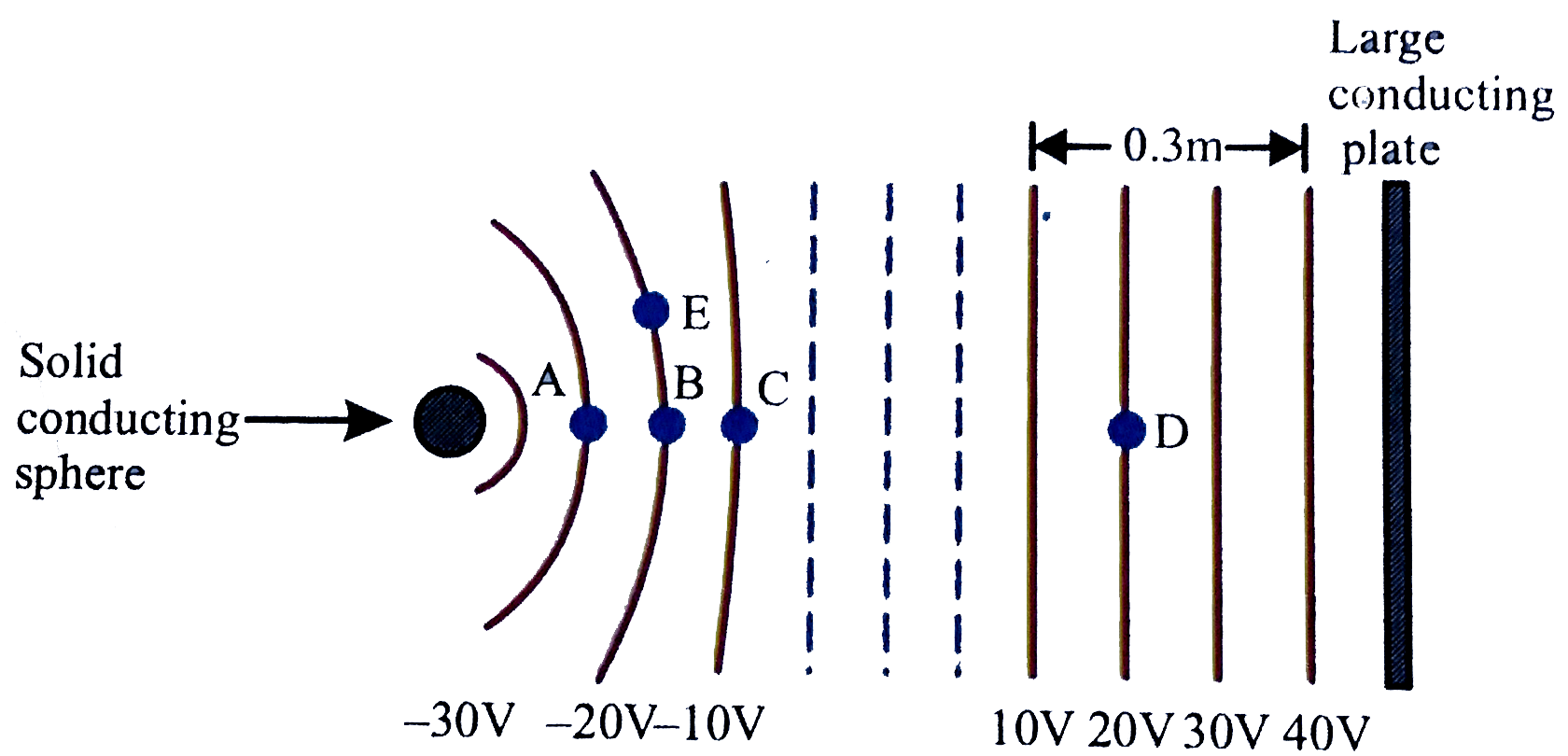
Surfaces charge density of the plate is equal to
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionConsider the Gaussian surface that surrounds parts of the charge distribution shown in figure. Then the contribution to the electric field at point P arises from charges

View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View SolutionCalculate the electric dipole moment of a system comprising of a charge + q distributed uniformly on a semicircular arc or radius R and a point charge – q kept at its centre.
View SolutionA charge is distributed with a linear density λ over a rod of the length L placed along radius vector drawn from the point where a point charge q is located. The distance between q and the nearest point on linear charge is R. The electrical force experienced by the linear charge due to q is
View SolutionTwo points charges +4 and +q are separated by distance r, where should a third point charge Q be placed that the whole system remains in equilibrium
View SolutionConsider a point charge +q placed at the origin and another point charge -2p placed at a distance of 9 m from the charge +q . Determine the point between the two charges at which electric potential is zero.
View SolutionConsider the figure given below
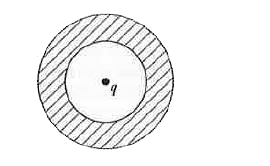
A charge Q is placed inside the Spherical conductor shell. In the given table, column 1 shows different charges, column 2 shows the positions of the electric charge and column 3 shows the different types of charge distribution.

In which case will the charge distribution be non-uniform ?
View SolutionConsider the figure given below
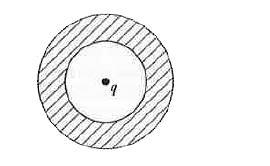
A charge Q is placed inside the Spherical conductor shell. In the given table, column 1 shows different charges, column 2 shows the positions of the electric charge and column 3 shows the different types of charge distribution.

In which case will the Charge distribution be uniform ?
View SolutionA charge is distributed with a linear density lamda over a rod of the length L placed along radius vector drawn from the point where a point charge q is located. The distance between q and the nearest point on linear charge is R. The electrical force experienced by the linear charge due to q is
View SolutionExamples On Charging||Discharging||Distribution OF charges on two Spheres
View SolutionConsider the Gaussian surface that surrounds parts of the charge distribution shown in figure. Then the contribution to the electric field at point P arises from charges
View Solution
