In the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its mid point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released.
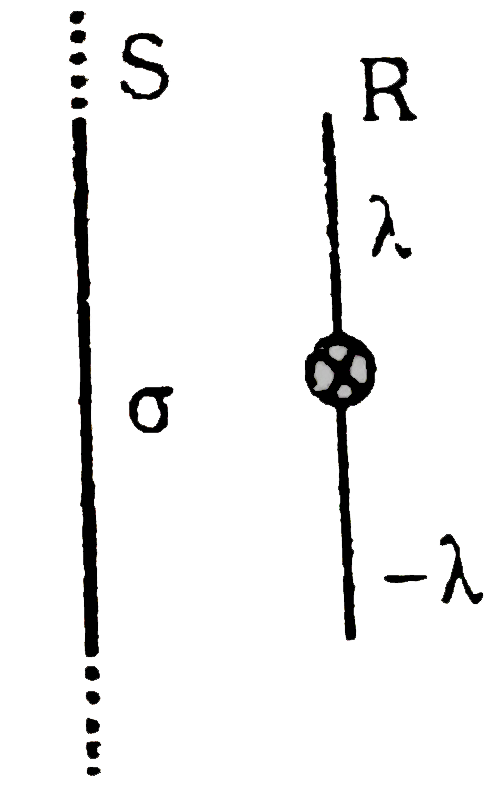 Solution in Gujrati
Solution in Gujrati
The correct Answer is:3σλ2m∈0
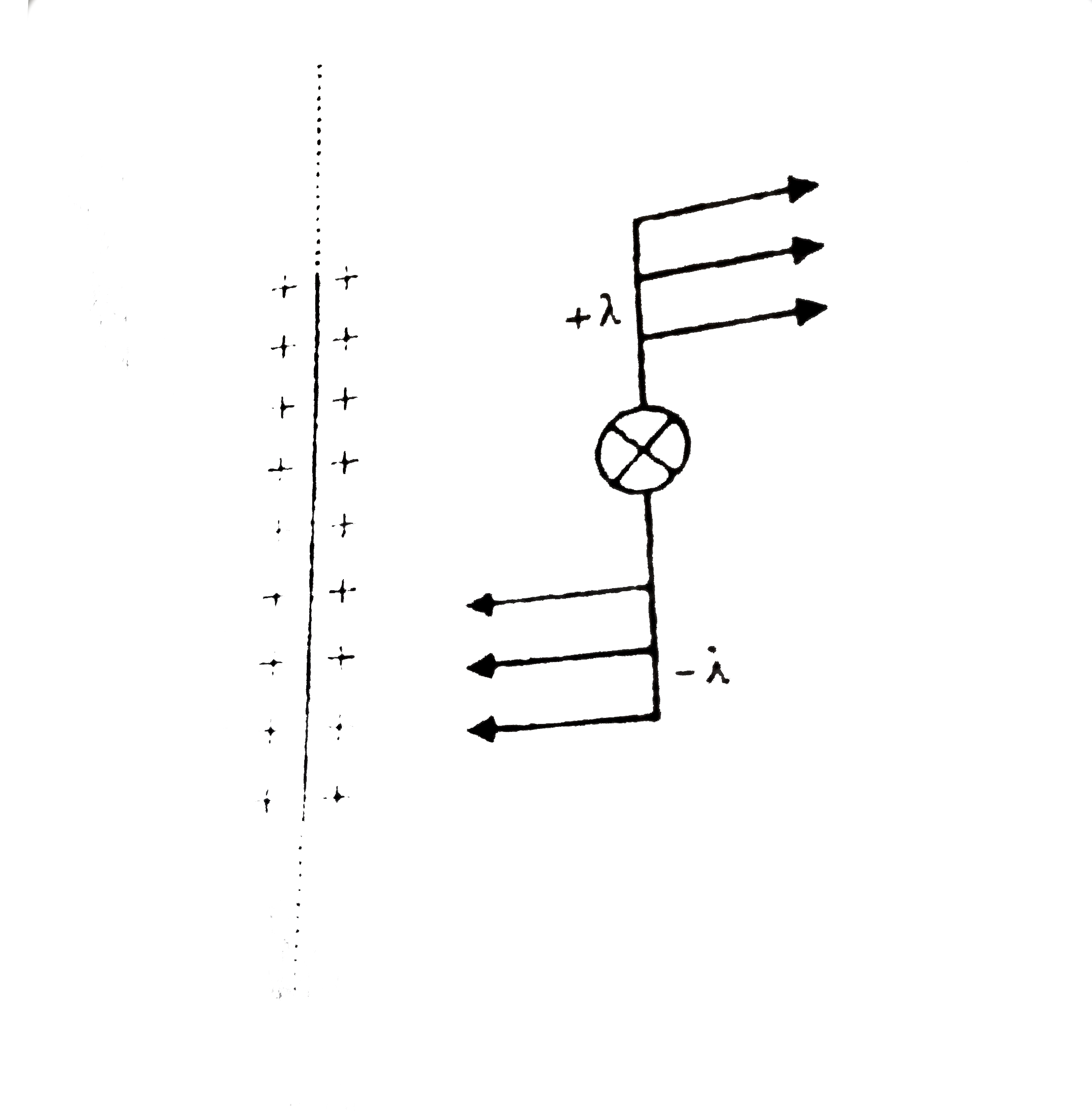
Net force on upper half=(λl2)(σ2∈0)
Torque on upper half=(λl2)×σ2∈0×l4
[l4= distance from hinge point for centre of mass]
total torque on rod
=λl2×σ2∈0×l4×2=Iα=ml212∝∴α=3λσ2m∈0
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exersice-04[B]
16 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(A)
35 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Comprehension 9
2 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
Two small balls having the same mass and charge and located on the same vertical at heights h1 and h2 are thrown in the same direction along the horizontal at the same velocity v. The first ball touches the ground at a horizontal distance R from the initial vertical position. At what height h2 will the second ball be at this instant? Neglect any frictional resistance of air and the effect of any induced charge on the ground.
View SolutionOn moving a charge of 20 coulomb by 2cm, 2J of work is done , the potential difference between the points is .
View SolutionFlow cytometry, illustrated in the figure, is a technique used to sort cells by type. The cells are placed in a conducting saline solution which is then forced from a nozzle. The stream breaks up into small droplets, each containing one cell. A metal collar surrounds the stream right at the point where the droplets seprate from the stream. Charging the collar polarizes the conducting liquid, causing the droplets to become charged as they break off from the steam. A leser beam probes the solution just upstream from the charging collar, looking for the presence of certain types of cells. All droplets containing one particular type of cell are given the same charge by the charging collar. Droplets with other desired types of cells receive a different charge, and droplats with no desired cell receive no charge. The charged. The charges droplets then pass between two parallel charged electrodes where they receive a horizontal force that directs force that directs them into different collection tubes, depending on air charge.

View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionA large nonconducting sheet M is given a uniform charge density. Two unchared small metal rods A and B are placed near the sheet as shown in figure

View SolutionA large sheet carries uniform surface charge density σ . A rod of length 2l has a linear charge density lamba on one half and −λ on the second half. The rod is hinged at the midpoint O and makes an angle θ with the normal to the sheet. The torque experience by the rod is
View SolutionAn infinite nonconducting sheet has surface charge density s. There is a small hole in the sheet as shown in the figure. A uniform rod of length l having linear charge density lambda is hinged in the hole as shown. If the mass of the rod is m, then the time period of oscillation for small angular displacement is
View SolutionA uniform rod AB of mass m and length l is hinged at its mid point C. The left half (AC) of the rod has linear charge density −λ and the right half (CB) has +λ where λ is constant. A large non conducting sheet of uniform surface charge density σ is also present near the rod. Initially the rod is kept perpendicular to the sheet. The end A of the rod is initialy at a distance d. Now the rod is rotated by a small angle in the plane of the paper and released. Prove that the rod will perform SHM and find its time period.

View SolutionA uniform rod of mass m length l is attached to smooth hinge at end A and to a string at end B as shown in figure. It is at rest. The angular acceleration of the rod just after the string is cut is :

View SolutionIn the figure shown S is a large nonconducting sheet of uniform charge density sigma . A rod R of length l and mass 'm' is parallel to the sheet and hinged at its mid point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released.
View SolutionCalculate the potential due to a thin uniformly charged rod of length L at the poiot P shown in figure. The lioear charge density of the rod is lambda C//m
View SolutionIn the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released
[3σλ2m∈0]
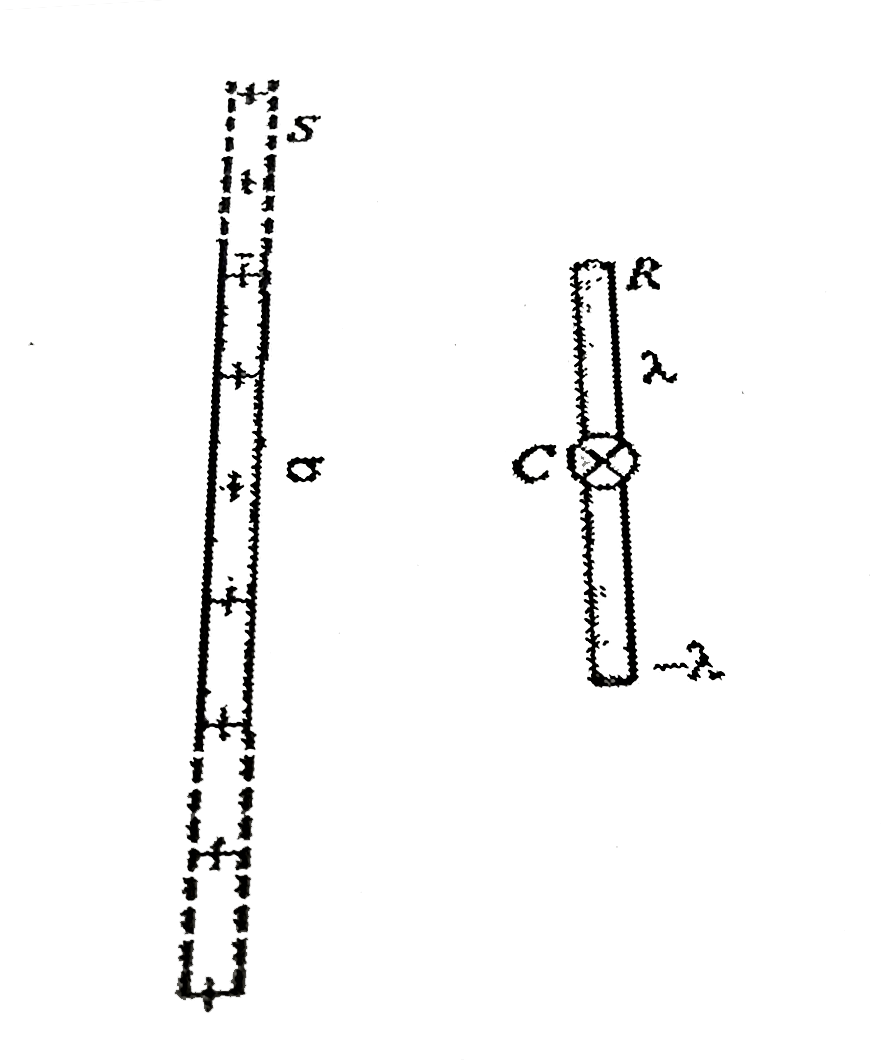
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:


View SolutionA large nonconducting sheet M is given a uniform charge density. Two unchared small metal rods A and B are placed near the sheet as shown in figure

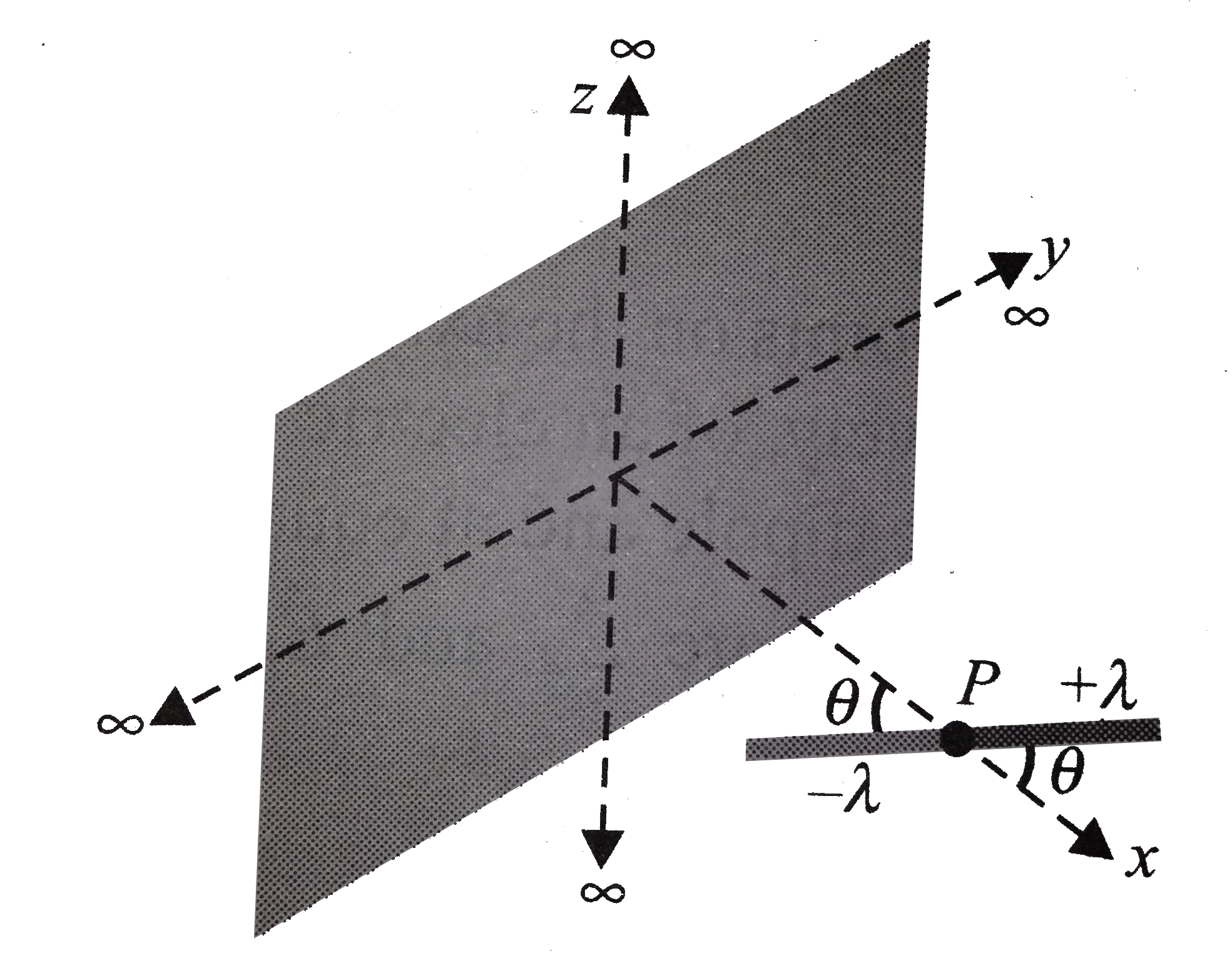
View SolutionAn infinite nonconducting sheet at x = 0 carries a uniform surface charge density σ. A thin rod of length 2L has a unifrom linear charge density λ on one half and λ on the other half. The rod is hinged at its mid point C at x = 2 L and lies in the XOZ plane making an angle α with the positive X-axis as shown in figure . The toqure →τ experienced by the rod is 4σλL2k∈0jsinα. The value of K is
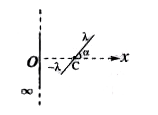
View Solution
