A positively charged thin metal ring of radius R is fixed in the xy plane with its centre at the origin O. A negatively charged particle P is released from rest at the point where . Then the motion of P isSolution in Gujrati
pariodic for all values of satisfying
simple harmonic for all values of satisfying
approximately simple harmonic provided
such that P crosses O and continues to move along negative z-axis towards
The correct Answer is:A, C
Let Q be the charge on the ring, the negative charge -q is released from point . The electric field at P due to the charged ring will be along positive z-axis and its magnitude will be
at centre of the ring because
Therefore, force on charge P will be towards centre as shown, and its magnitude is
...(i)
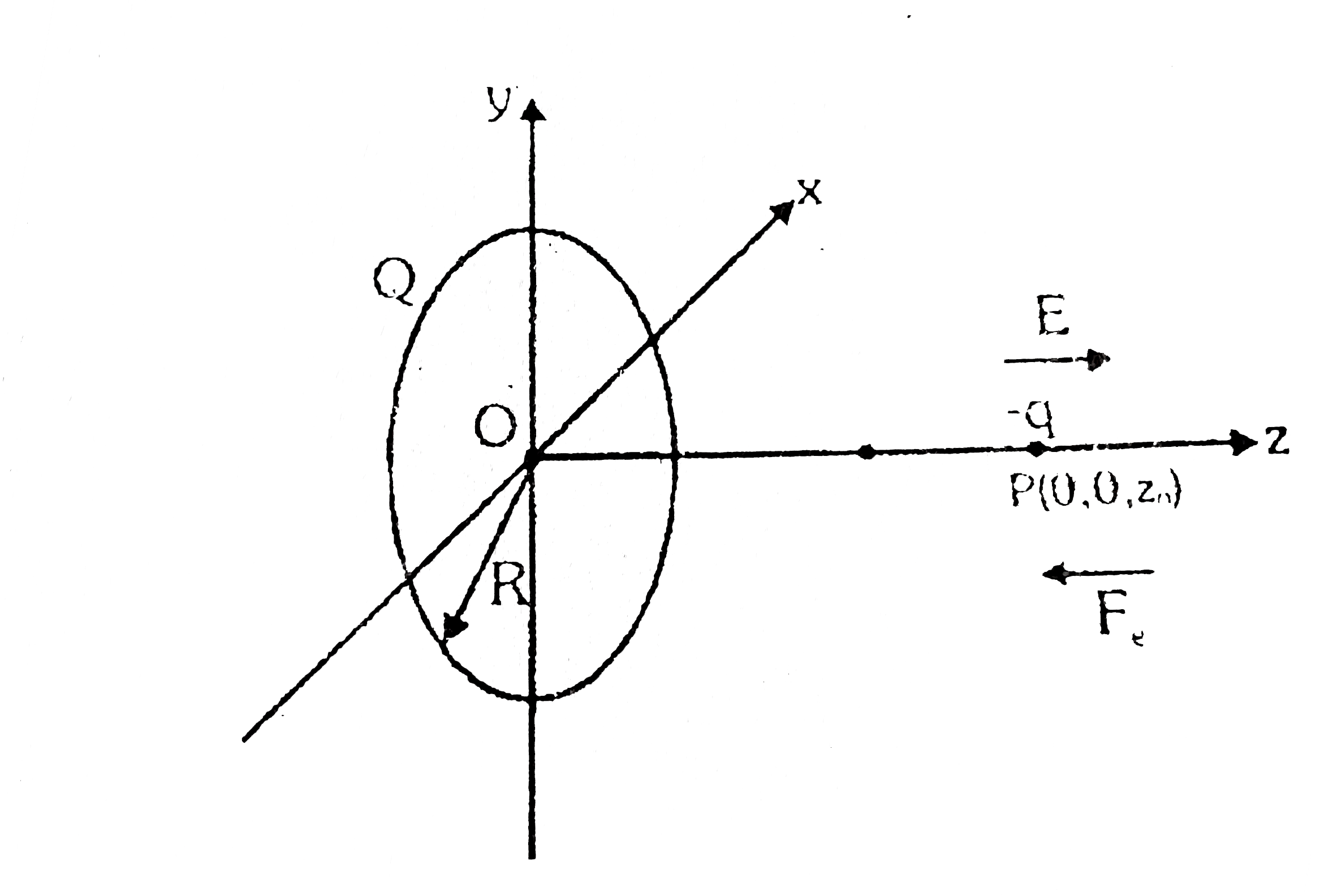
Similarly, when it courses the origin, the force is again towards centre O.
Thus, the motion of the particle is periodic for all values of lying between 0 and .
Secondly, if
(From Eq. 1)
i.e., the restoring force . Hence, the motion of the particle will be simple harmonic. (Here negative sign implies that the force is towards its mean position).
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - REASONING TYPE
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - MATCH THE COLUME TYPE
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(B)
19 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
statement 1 : For practical purposes, the earth is used as a reference at zero potencial in electrical circuits. statement 2 : The electrical potential of a sphere of radius R with charge Q uniformly distributed on the surface is given by Q4πε0R.
View SolutionFour charges Q1,Q2,Q3 and Q4 oof same magnitude are fixed along the x axis at x=−2a,−a,+a and +2a, respectively. A positive charge q is placed on the positive y axis at a distance b>0. Four options of the signs of these charges are given in List I. The direction of the forces on the charge q is given in List II. Match List I with List II and select the correct answer using the code given below the lists.

List-IList-II(P)Q1,Q2,Q3,Q4all positive(1)+x(Q)Q1,Q2 positive, Q3,Q4 negative(2)−x(R)Q1,Q4 positive ,Q2,Q3 negative(3)+y(S)Q1,Q3 positive , Q2,Q4 negative(4)−y
View SolutionA charge +q is fixed at each of the points x=x0, x=3x0, x=5x0,…………x=∞ on the x axis, and a charge −q is fixed at each of the points x=2x0, x=4x0, x=6x0, …………x=∞. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be Q/(4πε0r).Then, the potential at the origin due to the above system of
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionA positively charged thin metal ring of radius R is fixed in the xy plane with its centre at the origin O. A negatively charged particle P is released from rest at the point (0, 0, z_0) where z_0gt0 . Then the motion of P is
View SolutionSTATEMENT 1: When a negative charge -q is released at a distance R from the centre and along the axis of a uniformly and positvely charged fixed ring of radius R, the negative charge does oscillation but not SHM. STATEMENT 2: The force on negative charge is always towards the centre of the ring but it is not proportional to the displacement from the centre of the ring.
View SolutionA sermicircular ring of radius R carries a uniform linear charge of lamda . P is a point in the plane of the ring at a distance R from centre O. OP is perpendicular to AB. Find electric field intensity at point P.
View SolutionA thin circular ring of radius r is uniformly charged over its length.Consider two points,the centre of ring 0 ,and a point P on the axis of the ring at a distance a from the centre of the ring.If ratio of potential at points O and P is V0Vp=√101, then value of ar is ..
View SolutionA thin circular ring of radius r is uniformly charged over its length.Consider two points the centre of ring 0 and a point P on the axis of the ring at a distance a from the centre of the ring.If ratio of potential at points 0 and P is (V_(0))/(V_(p))=(sqrt(10))/(1) then value of (a)/(r) is
View SolutionA thin fixed ring of radius 'R' and positive charge 'Q' is placed in a vertical plane. A particle of mass 'm' and negative charge 'q' is placed at the centre of ring. If the particle is given a small horizontal displacement, show that it executes SHM. Also find the time period of small oscillations of this particle, about the centre of ring. (Ignore gravity)
View Solutionएक धन-आवेशित पतली धातु की वलय जिसकी त्रिज्या R है, x-y तल में स्थित है तथा इसका केन्द्र मूल बिन्दु् O पर है। एक ऋण आवेशित कण P बिन्दु (0,0,z0) से विरामावस्था से छोड़ा जाता है, जहाँ z0>0, तब P की गति है।
View SolutionA positively charged thin metal ring of radius R is fixed in the xy plane, with its centre at the origin O. A negatively charged particle P is released from rest at the point (0,0,z0) where z0>0. Then the motion of P is
a. Periodic for all value of z0 satisfying 0<z0<∞ M
b. Simple harmonic, for all values of Z0 satisfying 0<z0≤R
c. Approximately simple harmonic, provided z0<<R
d. Such that P crosses O and continues to move along the negative z-axis towards z=−∞
Choose the correct answer
View SolutionTwo equal negative charges -q are fixed at the points (0,alpha) and (0, -alpha) on the y-axis. A positive charge Q is released from rest at the point (2alpha, 0) on the x-axis. The charge Q will
View SolutionTwo equal negative charges -q are fixed at point (0, a) and (0, -a). A positive charge Q is released from rest at the point (2a, 0) on the x-axis. What type of oscillations does the charge Q execute?
View Solution
