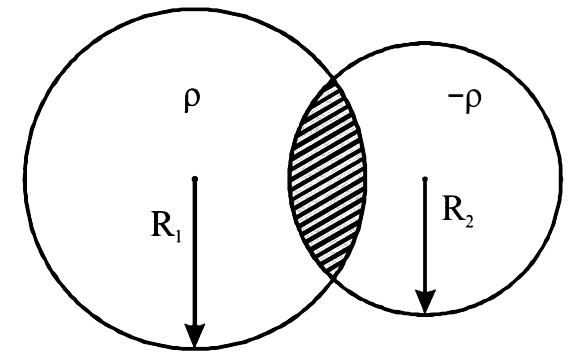
Two non-conducting spheres of radii R1 and R2 and carrying uniform volume charge densities +ρ and −ρ, respectively, are placed such that they partially overlap, as shown in the figure. At all points in the overlapping region
 Solution in Gujrati
Solution in Gujrati
the electrostatic field is zero
the electrostatic potential is constant
the electrostatic field is constant in magnitude
the electrostatic field has same direction
The correct Answer is:C, D
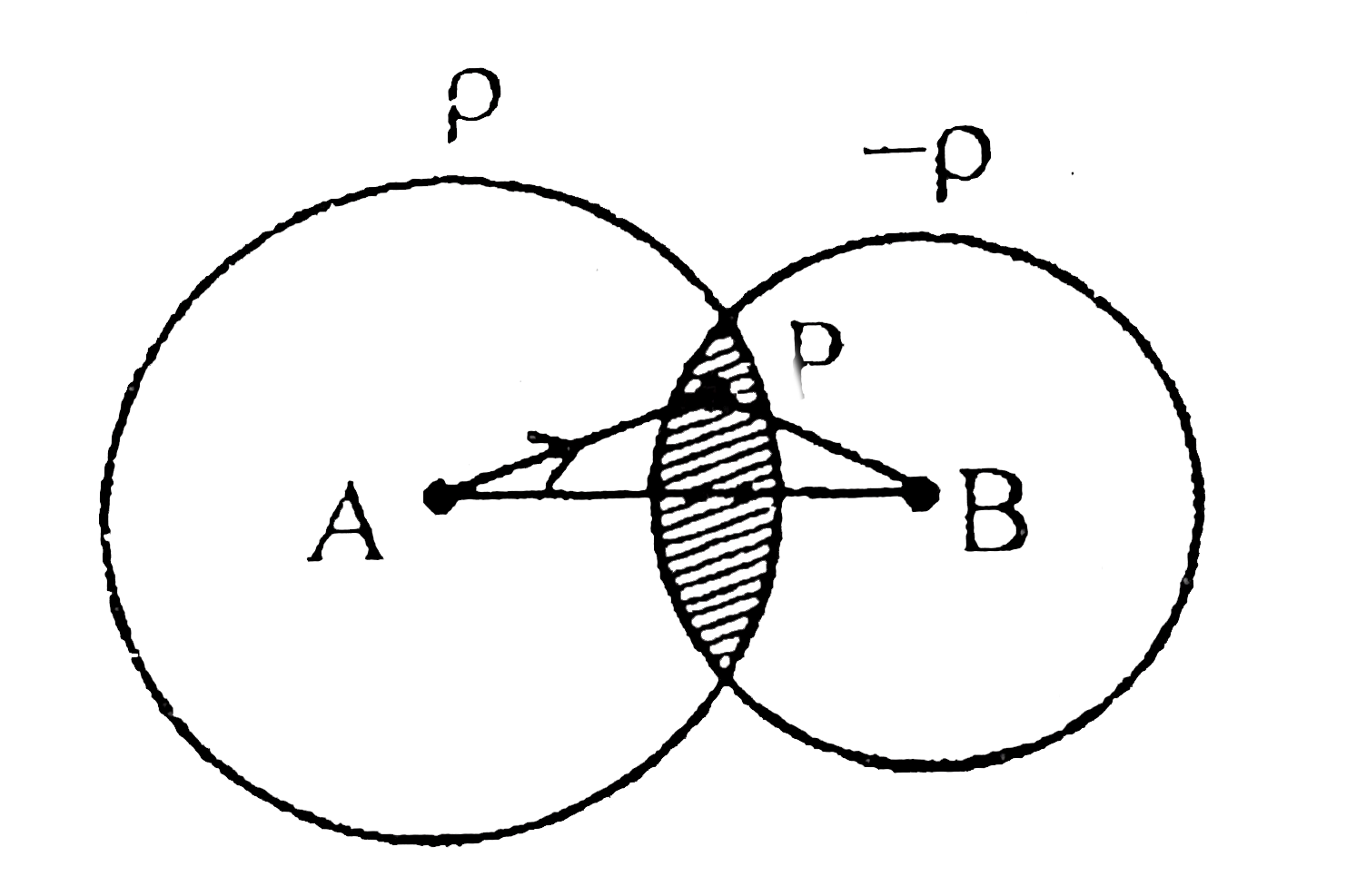
electric field at point P
=ρ(−−→AP)3∈0+−ρ(−−→BP)3∈0=ρ(−−→AP−−−→BP)3∈0=ρ(−−→AB)3∈0
= constant in both magnitude and direction at evergy point of overlap region.
also e is non zero so potential is not same at all points.
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - REASONING TYPE
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - MATCH THE COLUME TYPE
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(B)
19 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
statement 1 : For practical purposes, the earth is used as a reference at zero potencial in electrical circuits. statement 2 : The electrical potential of a sphere of radius R with charge Q uniformly distributed on the surface is given by Q4πε0R.
View SolutionFour charges Q1,Q2,Q3 and Q4 oof same magnitude are fixed along the x axis at x=−2a,−a,+a and +2a, respectively. A positive charge q is placed on the positive y axis at a distance b>0. Four options of the signs of these charges are given in List I. The direction of the forces on the charge q is given in List II. Match List I with List II and select the correct answer using the code given below the lists.

List-IList-II(P)Q1,Q2,Q3,Q4all positive(1)+x(Q)Q1,Q2 positive, Q3,Q4 negative(2)−x(R)Q1,Q4 positive ,Q2,Q3 negative(3)+y(S)Q1,Q3 positive , Q2,Q4 negative(4)−y
View SolutionA charge +q is fixed at each of the points x=x0, x=3x0, x=5x0,…………x=∞ on the x axis, and a charge −q is fixed at each of the points x=2x0, x=4x0, x=6x0, …………x=∞. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be Q/(4πε0r).Then, the potential at the origin due to the above system of
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density rho=A/r , where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
View SolutionThere are two nonconducting spheres having uniform volume charge densities rho and - rho . Both spheres have equal radius R . The spheres are now laid down such that they overlap as shown in Fig.2.125. Take vec(d) = O_(1) vec(O_(2)) . The electric field vec(E) in the overlapped region is
View SolutionA Uniformly charged solid non-conducting sphere of uniform volume charge density rho and radius R is having a concentric spherical cavity of radius r. Find out electric field intensity at following points, as shown in the figure : (i) Point A (ii) Point B (iii) Point C (iv) Centre of the sphere
View SolutionTwo non-conducting spheres of radii R_(1) and R_(2) and carrying uniform volume charge densities +rho and - rho respectively are placed such that they partially overlapping region.
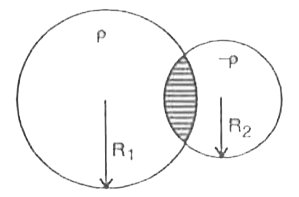
View Solutionदो अचालक R1 तथा R2 त्रिज्या वाले गोलों को क्रमशः +ρ तथा −ρ एकसमान आयतन आवेश घनत्व से आवेशित किया गया है। इन गोलों को चित्र में दर्शाय अनुसार इस प्रकार जोड़ कर रखा गया है कि वे आंशिक रूप से आच्छादित है। आच्छादित क्षेत्र के प्रत्येक बिन्दु पर-
View Solutionचार संकेंद्रित गोले A,B,C और D त्रिज्या क्रमशः a,2a,3a तथा 4a हैं। कोश B और D को क्रमशः +q और −q आवेश दिए गए हैं। गोले C अब भूसम्पर्कन पर है। तब VA−VC
View Solutionsigma and rho are surface and volume charge densities respectively of a charged sphere, so,......
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), has volume charge density rho =A/r , where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant is :
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
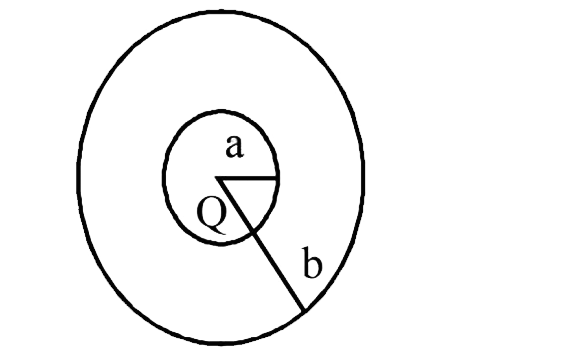
View SolutionThe region between two concentric spheres of radii ‘a’ and ‘b’, respectively (see figure), has volume charge density p=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is :
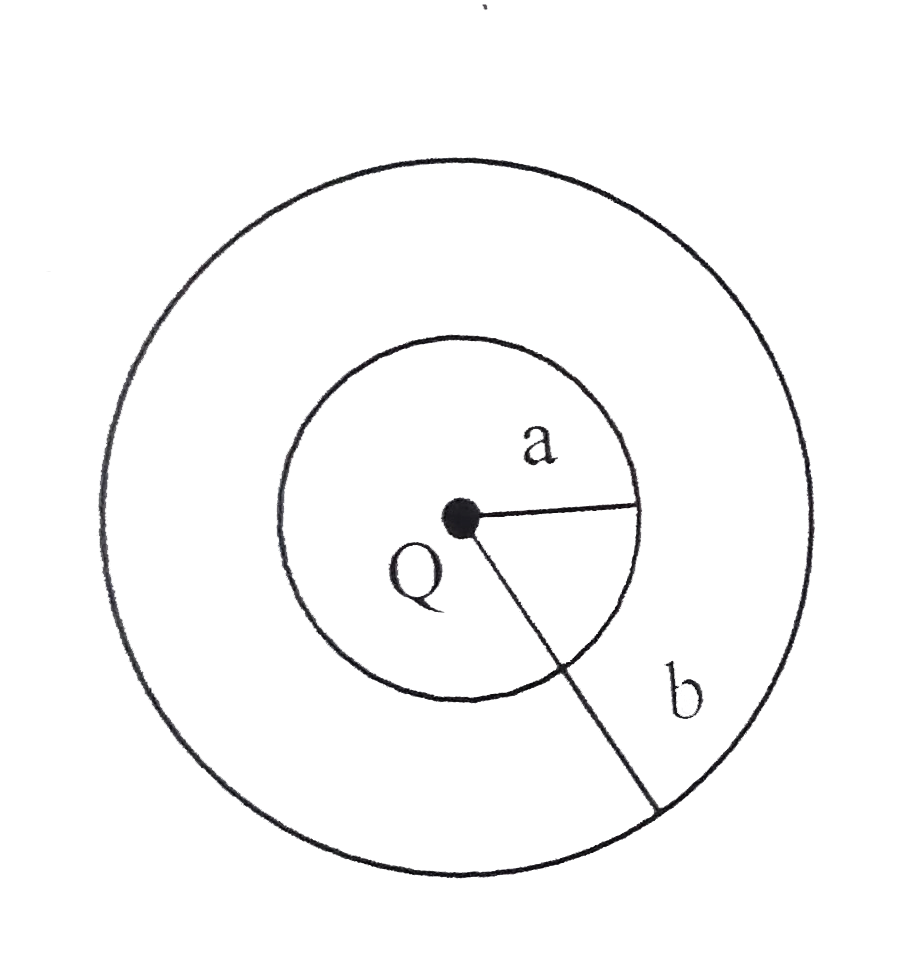
View SolutionThere are two nonconducting spheres having uniform volume charge densities rho and - rho . Both spheres have equal radius R . The spheres are now laid down such that they overlap as shown in Fig.2.125. Take vec(d) = O_(1) vec(O_(2)) . The electric field vec(E) in the overlapped region is
View Solution
