Consider the following sketch of potential energy for a particle as a function of position. There are no dissipative forces or internal sources of energy.

What is the minimum total mechanical energy that the particle can have if you know that it has travelled over the entire region of X shown?Solution in Gujrati
−8
6
10
It depends on direction of travel
The correct Answer is:C
If particle can reach point 'd', then it can travel over the entire region.
Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLEN CHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Choose the correct statement:
View SolutionChoose the correct statement:
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionWhy are electric field lines perpendicular at a point on an equipotential surface of a conductor ?
View SolutionA linear harmonic oscillator has a total mechanical energy of 200 J . Potential energy of it at mean position is 50J . Find (i) the maximum kinetic energy, (ii)the minimum potential energy, (iii) the potential energy at extreme positions.
View SolutionFigure shows the variation of potential energy of a particle as a function of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values of x, U is zero, i.e., xlarr10 and xgt15 , U=0 . If the total mechanical energy of the particle is -40J , then it can be found in region
View SolutionFigure shows the variation of potential energy of a particle as a function of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values of x, U is zero, i.e., xlarr10 and xgt15 , U=0 . If the particle is isolated and its total mechanical energy is 60J , then
View SolutionA potential energy curve U(x) is shown in the figure. What value must the mechanical energy E_(mec) of the particle not exceed, if the particle is to be trapped within the region shown in graph? .
View SolutionPotential energy curve U of a particle as function of the position of a particle is shown. The particle has total mechanical energy E of 3.0 joules. Then select correct alternative.
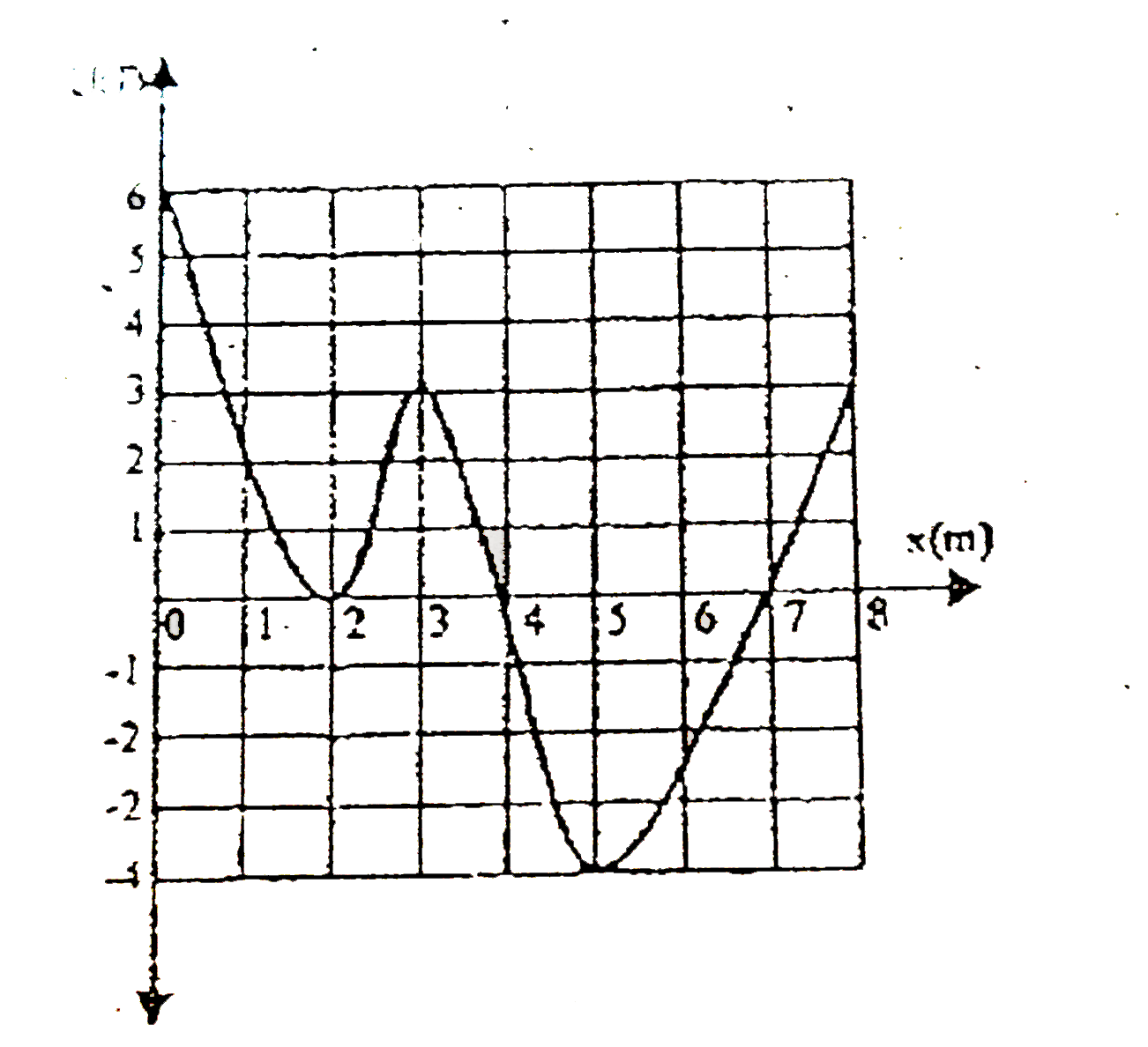
View SolutionForce acting on a particle is F=−8x in S.H.M. The amplitude of oscillation is 2 (in m) and mass of the particle is 0.5 kg. The total mechanical energy of the particle is 20 J. Find the potential energy of the particle in mean position (in J).
View SolutionA particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
View SolutionA particle with total energy E is moving in a potential energy region U (x). Motion of the particle is restricted to the region when
View SolutionForce acting on a particle is F--8x in SHM, The amplitude of oscillations is 2 (in m) and mass of the particle is 0.5kg. The total mechanical energy of the particle is 20J. Find the potential energy of the particle in mean position (in J).
View SolutionA linear harmonic oscillator has a total mechanical energy of 200 J . Potential energy of it at mean position is 50J . Find (i) the maximum kinetic energy, (ii)the minimum potential energy, (iii) the potential energy at extreme positions.
View SolutionA linear harmonic oscillator has a total mechanical energy of 200 J . Potential energy of it at mean position is 50J . Find (i) the maximum kinetic energy, (ii)the minimum potential energy, (iii) the potential energy at extreme positions.
View SolutionFigure shows the variation of potential energy of a particle as a function of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values of x, U is zero, i.e., x←10 and x>15, U=0.

If the particle is isolated and its total mechanical energy is 60J, then
View Solution
