A partical of mass 2kg is moving on the x−axis with a constant mechanical energy 20J. Its potential energy at any x is U=(16−x2)J where x is in metre. The minimum velocity of particle is :−Solution in Gujrati
2m/s
4m/s
6m/s
zero
The correct Answer is:A
From expression of potential energy Maximum
PE=16J so minimum KE=4J
Therefore 12×2×v2=4⇒v=2m/s
Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLEN CHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Choose the correct statement:
View SolutionChoose the correct statement:
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionWhy are electric field lines perpendicular at a point on an equipotential surface of a conductor ?
View SolutionA single conservative fore F_(x) acts on a 2kg particle that moves along the x-axis. The potential energy is given by. U =(x-4)^(2)-16 Here, x is in metre and U in joule. At x =6.0 m kinetic energy of particle is 8 J find . (a) total mechanical energy (b) maximum kinetic energy (c) values of x between which particle moves (d) the equation of F_(x) as a funcation is zero (e) the value of x at which F_(x) is zero .
View SolutionThe potential energy of a particle moving along x-axis is given by U = 20 + 5 sin (4 pi x) , where U is in J and x is in metre under the action of conservative force :
View SolutionA single conservative f_((x)) acts on a m = 1 kg particle moving along the x-axis. The potential energy U_((x)) is given by : U_((x)) = 20 + (x - 2)^(2) where x is in metres. At x = 5 m , a particle has kintetic energy of 20 J The maximum speed of the particle is:
View SolutionA single conservative f_((x)) acts on a m = 1 kg particle moving along the x-axis. The potential energy U_((x)) is given by : U_((x)) = 20 + (x - 2)^(2) where x is in metres. At x = 5 m , a particle has kintetic energy of 20 J The minimum speed of the particle is:
View SolutionA single conservative f(x) acts on a m=1kg particle moving along the x-axis. The potential energy U(x) is given by :
U(x)=20+(x−2)2
where x is in metres. At x=5m, a particle has kintetic energy of 20 J
The maximum value of potential energy is:
View SolutionA single conservative f_((x)) acts on a m = 1 kg particle moving along the x-axis. The potential energy U_((x)) is given by : U_((x)) = 20 + (x - 2)^(2) where x is in metres. At x = 5 m , a particle has kintetic energy of 20 J The largest value of x will be:
View SolutionA single conservative f(x) acts on a m=1kg particle moving along the x-axis. The potential energy U(x) is given by :
U(x)=20+(x−2)2
where x is in metres. At x=5m, a particle has kintetic energy of 20 J
The position of equilibrium and its nature is:
View SolutionA single conservative force F(x) acts on a particle that moves along the x - axis. The graph of the potential energy with x is given. At x=5m, the particle has a kinetic energy of 50 J and its potential energy is related to position 'x' as U=15+(x−3)2 Joule where x is in meter. Then:
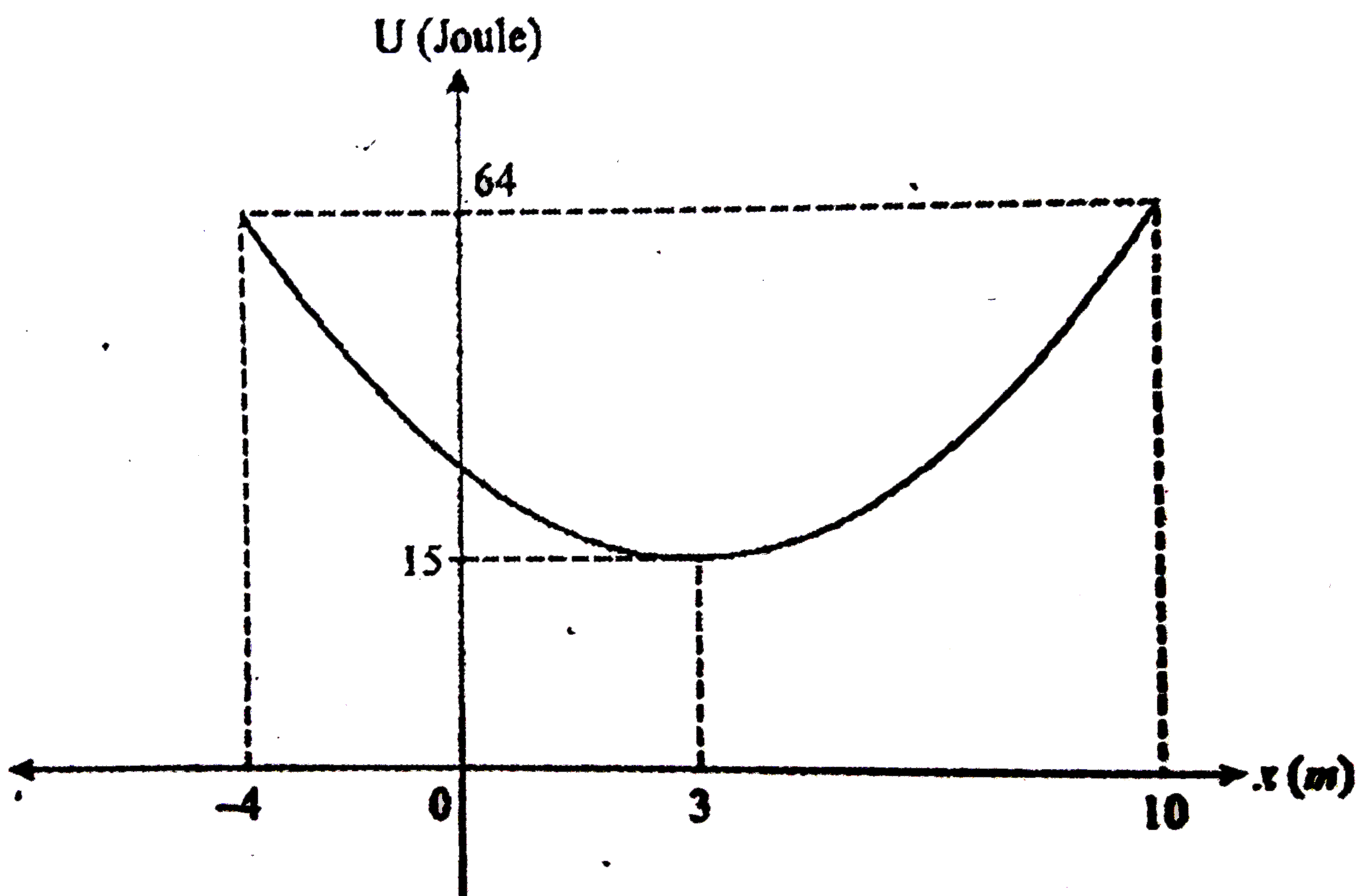
View SolutionThe potential energy of a particle of mass 1 kg moving along x-axis given by U(x)=[x22−x]J. If total mechanical speed (in m/s):-
View SolutionThe potential energy of particle of mass 1kg moving along the x-axis is given by U(x)=16(x2−2x) J, where x is in meter. Its speed at x=1 m is2m/s. Then,
View SolutionThe potential energy of 1kg particle free to move along x-axis is given by U(x)=[x^4/4-x^2/2]J. The total mechanical energy of the particle is 2J. The maximum speed of the particle is
View SolutionThe total mechanical energy of a 2.00 kg particle moving along an x axis is 5.00 J. The potential energy is given as U(x)=(x4−2.00x2)J, with x in meters. Find the maximum velocity.
View Solution
