Position vector →r of a particle varies with time t accordin to the law →r=(12t2)ˆi−(43t3)ˆj+(2t)ˆk, where r is in meters and t is in seconds. Find suitable expression for its velocity and acceleration as function of timeSolution in Gujrati
The ball projected with velocity →u=uxˆi+uyˆj from O reachrs the point P with velocity →v=uxˆi+vyˆj and hits the ground at point Q at the instant T=4+5=9s as shown in the adjoining motion diagram.
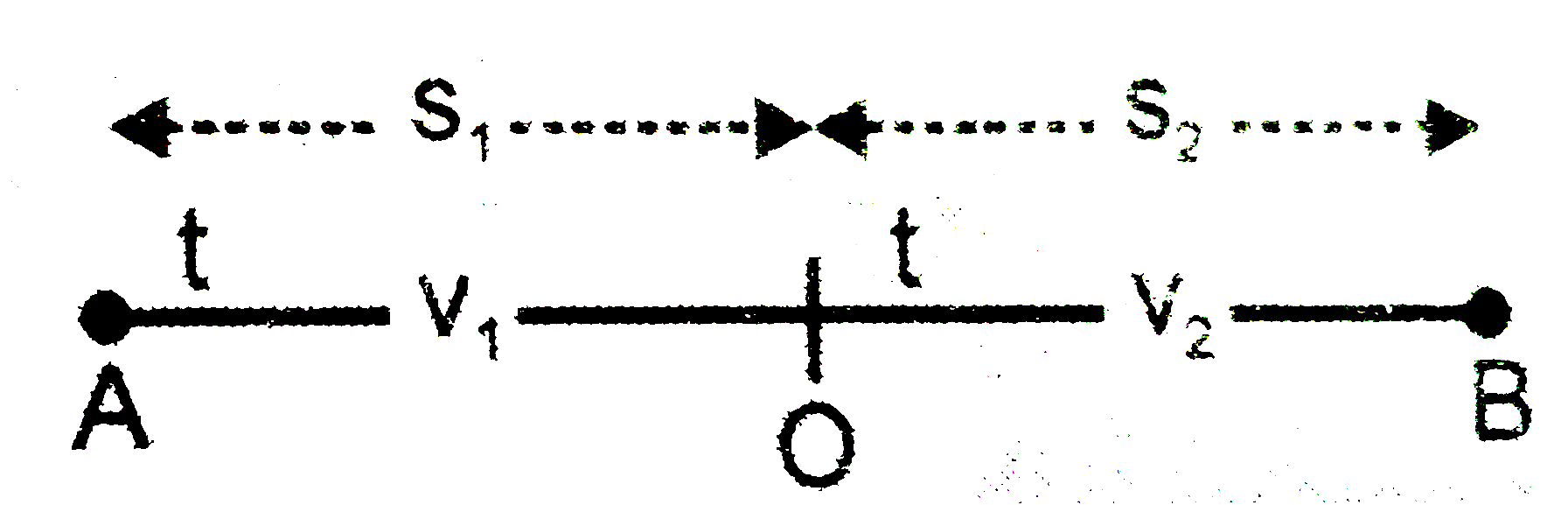
From equation of time of flight, we have its initial y-component of velocity uy
T=2uyg→uy=12gT
Substituting above in eq. (ii) and rearranging terms, we have the height y of the point P.
y=uyt−12gt2→y=12gt(T−t)=12×9.8×4(9−4)=98m
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-01
55 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-02
57 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A bird moves from point (1,−2,3) to (4,2,3). If the speed of the bird id 10m/s, then the velocity of the bird is :-
View SolutionA particle is moving in a plane with velocity given by →u=u0ˆi+(aωcosωt)ˆj, where ˆi and ˆj are unit vectors along x and y axes respectively. If particle is at the origin at t=0. Calculate the trajectory of the particle :-
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionA particle move in x−y plane such that its position vector varies with time as →r=(2sin3t)ˆj+2(1−cos3t)ˆj. Find the equation of the trajectory of the particle.
View SolutionThe position vector of a particle is given by vec(r)=1.2 t hat(i)+0.9 t^(2) hat(j)-0.6(t^(3)-1)hat(k) where t is the time in seconds from the start of motion and where vec(r) is expressed in meters. For the condition when t=4 second, determine the power (P=vec(F).vec(v)) in watts produced by the force vec(F)=(60hat(i)-25hat(j)-40hat(k)) N which is acting on the particle.
View SolutionPosition vector →r of a particle varies with time t accordin to the law →r=(12t2)ˆi−(43t1.5)ˆj+(2t)ˆk, where r is in meters and t is in seconds.
(a) Find suitable expression for its velocity and acceleration as function of time (b) Find magnitude of its displacement and distance traveled in the time interval t=0 to 4s.
View SolutionA particle moves along the space curve vec(r)=(t^(2)+t)hat(i)+(3t-2)hat(j)+(2t^(3)-4t^(2))hat(k) . (t in sec, r in m ) Find at time t=2 the (a) velocity, (b) acceleration, (c) speed or magnitude of velocity and (d) magnitude of acceleration.
View SolutionPosition vector of a particle is expressed as function of time by equation vec(r)=2t^(2)+(3t-1) hat(j) +5hat(k) . Where r is in meters and t is in seconds.
View SolutionFind the shortest distance between the given line
→r=(3−t)ˆi+(4+2t)ˆj+(t−2)ˆk
→r=(1+s)ˆi+(3s−7)ˆj+(2s−2)ˆk
View Solutionकिसी कण की स्थिति निम्न समीकरण द्वारा दी जाती है -
→r=3tˆi+2t2ˆj+5ˆk
जहाँ r मीटर में तथा t सेकंड में है। निम्न की गणना कीजिए-
समय t पर वेग व त्वरण
View Solutionकिसी कण की स्थिति निम्न समीकरण द्वारा दी जाती है -
→r=3t→i+2t2ˆj+5ˆk
जहाँ r मीटर में तथा t पर सेकंड में है। निम्न की गणना कीजिए-
समय t = 1 सेकंड पर वेग का परिमाण व दिशा |
View Solutionएक कण के स्थिति सदिश को S.I. मात्रक में समय के फलां के रूप में नीचे व्यक्त किया गया है -
→r=t3ˆi+4t2ˆj+7ˆk
कण का तात्क्षणिक वेग तात्क्षणिक त्वरण को समय के फलन रूप में व्यक्त कीजिए।
View SolutionA particle move in x−y plane such that its position vector varies with time as →r=(2sin3t)ˆj+2(1−cos3t)ˆj. Find the equation of the trajectory of the particle.
View SolutionThe time dependence of the position of a particle of mass m = 2 is given by →r(t)=2tˆi−3t2ˆj Its angular momentum, with respect to the origin, at time t = 2 is :
View Solution
