A projectile is projected with some initial velocity and some initial angle of projection. A wind is also blowing, due to which constant horizontal retardation a is imparted to the particle in the plane of motion. It is found that, the particle is at same height at two different time t1 & t2 and particle is at same horizontal distance at two different time t3 & t4
Angle of projection of particle is :-Solution in Gujrati
tan−1(t1+t2t3+t4)
tan−1[a(t1+t2)g(t3+t4)]
tan−1[g(t1+t2)a(t3+t4)]
None of these
The correct Answer is:C
In vertical direction h=(usinθ)t−12gt2
⇒t2−(2usinθg)t+2hg=0
⇒t1+t2=2usinθg …(i)
In horizontal direction x=(ucosθ)t−12at2
⇒t2−(2ucosθa)t+2xa=0
⇒t3+t4=2ucosθa...(ii)
From (i) and (ii) θ=tan−1[g(t1+t2)a(t3+t4)]
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-04[A]
35 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Exercise-04[B]
14 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Comprehension#6
4 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
Fig. 2 (NCT).9 show the x−t plot of a particle in one dimensional motion. Three different equal intervals of time are shown. In which interval the average speed is greatest and in which it is the least ? Give th sign of average speed for each interval.
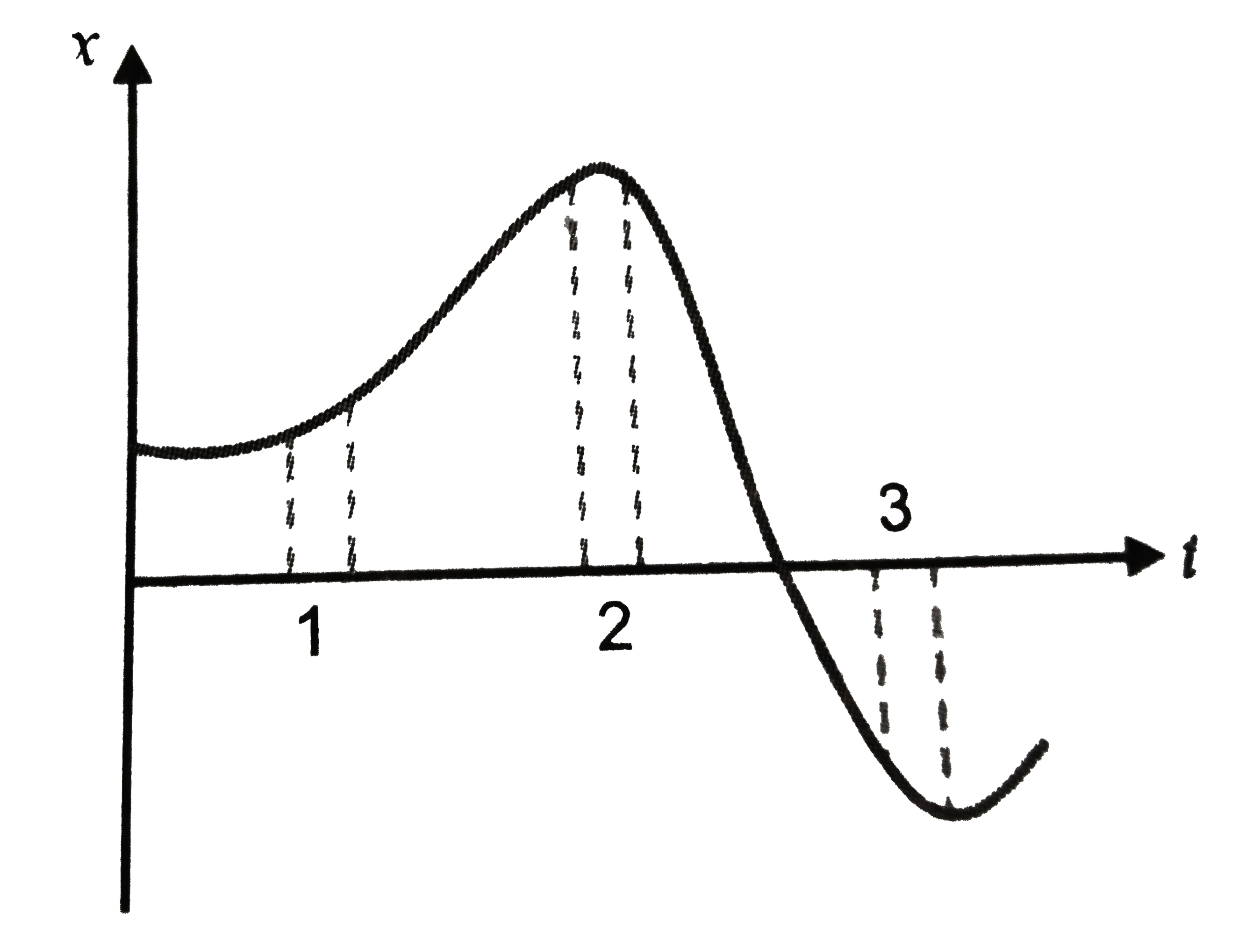 .
.
View SolutionTwo towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20kmh−1 in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road ?
View SolutionWhen a particle is undergoing motion, the diplacement of the particle has a magnitude that is equal to or smaller than the total distance travelled by the particle. In many cases the displacement of the particle may actually be zero, while the distance travelled by it is non-zero. Both these quantities, however depend on the frame of reference in which motion of the particle is being observed. Consider a particle which is projected in the earth's gravitational field, close to its surface, with a speed of 100√2m/s, at an angle of 45∘ with the horizontal in the eastward direction. Ignore air resistance and assume that the acceleration due to gravity is 10m/s2.
The motion of the particle is observed in two different frames: one in the ground frame (A) and another frame (B), in which the horizontal component of the displacement is always zero. Two observers locates in these frames ill agree on :-
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionTwo particles are projected from the same point with the same speed at different angles θ1 and θ2 to the horizontal. If their respective times of flights are T1 and T2 and horizontal ranges are same then
a) θ1+θ2=90∘ ,
b)T1=T2tanθ1
c.T1=T2tanθ2 ,
d) T1sinθ2=T2sinθ1
View SolutionTwo particle are projected with same initial velocities at an angle 30^(@) and 60^(@) with the horizontal .Then
View SolutionA projectile has the same range R for two angles of projections but same speed. If T1 and T2 be the times of flight in the two cases, then
Here θ is the angle of projection corresponding to T1.
View SolutionFor a given velocity, a projectile has the same range R for two angles of projection. If t1 and t2 are the time of flight in the two cases, then t1=t2 is equal to
View SolutionWhen a particle is projected at an angle to the horizontal, it has range R and time of flight t_(1) . If the same projectile is projected with same speed at another angle to have the saem range, time of flight is t_(2) . Show that: t_(1)t_(2)=(2R//g)
View SolutionA particle is projected in air with an initial velocity u directed at an angle theta above horizontal. After time t_(0) the velocity of the particle is directed at angle phi above horizontal.
View SolutionAn object projected with same speed at two different angles covers the same horizontal range R. If the two times of flight be t1andt2 . The range is 1αgt1t2, the value of α is
View SolutionA particle is projected with speed u at angle theta with horizontal from ground . If it is at same height from ground at time t_(1) and t_(2) , then its average velocity in time interval t_(1) to t_(2) is
View SolutionA projectile has same range R for the two angles of projection. If T_(1) and T_(2) are the times of flight in two cases, then:
View SolutionFor a given velocity, a projectile has the same range R for two angles of projection if t1andt2 are the time of flight in the two cases then
View SolutionTwo particles are projected from the same point with the same speed at different angles theta_(1) and theta_(2) to the horizontal. If their respective times of flights are T_(1) , and T_2 and horizontal ranges are same then
View Solution
