A balloon rises up with constant net acceleration of 10m/s2. After 2 s a particle drops from the balloon. After further 2 s match the following : (Takeg=10m/s2)
Column IColumn II(A)Height of perticle from ground(p)Zero(B)Speed of particle(q)10SIunits(C)Displacement of Particle(r)40SIunits(D)Acceleration of particle(s)20SIunitsSolution in Gujrati
The correct Answer is:(A)-r, (B)-p, (C)-s, (D)-q
Velocity & height of the bolloon after 2 sec:
v=0+10×2=20m/s↑⏐h=1/2×10×4=20m
Initial velocity of drop particle is equal to the velocity of balloon =20m
∵us=20m/sas=g⏐↓
After further 2svs=0
∴ height =us+vs2×2=20m from initial position of balloon
∴ Height from ground =20+2v=40m
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Assertion-Reason
20 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Comprehension#1
3 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-02
57 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
Assertion: A projectile is thrown with an initial velocity of (aˆi+bˆj)m/sec. If range of projectile is maximum then a=b.
Reason: In projectile motion, angle of projection is equal to 45∘ for maximum rang econdition.
View SolutionDistance is a scalar quantity. Displacement is a vector quqntity. The magnitude of displacement is always less than or equal to distance. For a moving body displacement can be zero but distance cannot be zero. Same concept is applicable regarding velocity and speed. Acceleration is the rate of change of velocity. If acceleration is constant, then equations of kinematics are applicable for one dimensional motion under the gravity in which air resistance is considered, then the value of acceleration depends on the density of medium. Each motion is measured with respect of frame of reference. Relative velocity may be greater/ smaller to the individual velocities.
A particle moves from A to B. Then the ratio of distance to displacement is :-
View SolutionA particle is moving in a plane with velocity given by →u=u0ˆi+(aωcosωt)ˆj, where ˆi and ˆj are unit vectors along x and y axes respectively. If particle is at the origin at t=0. Calculate the trajectory of the particle :-
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionA particle is projected from ground with velocity 40(sqrt2) m//s at 45^@ . Find (a) velocity and (b) displacement of the particle after 2 s. (g = 10 m//s^2)
View SolutionIn the diagram shown in figure, match the following (g=10m/s2)

Column-IColoumn-II(A)Acceleration of 2kg block(P)8 Si unit(B)Net force on 3kg block(Q)25 SI unit(C)Normal reaction between 2 kg and 1kg(R)2 SI unit(D)Normal reaction between 3 kg and 2kg (S) 45 SI unit(T) None
View SolutionFor the velocity -time graph shown in figure, in a time interval from t=0 to t=6s, match the following:
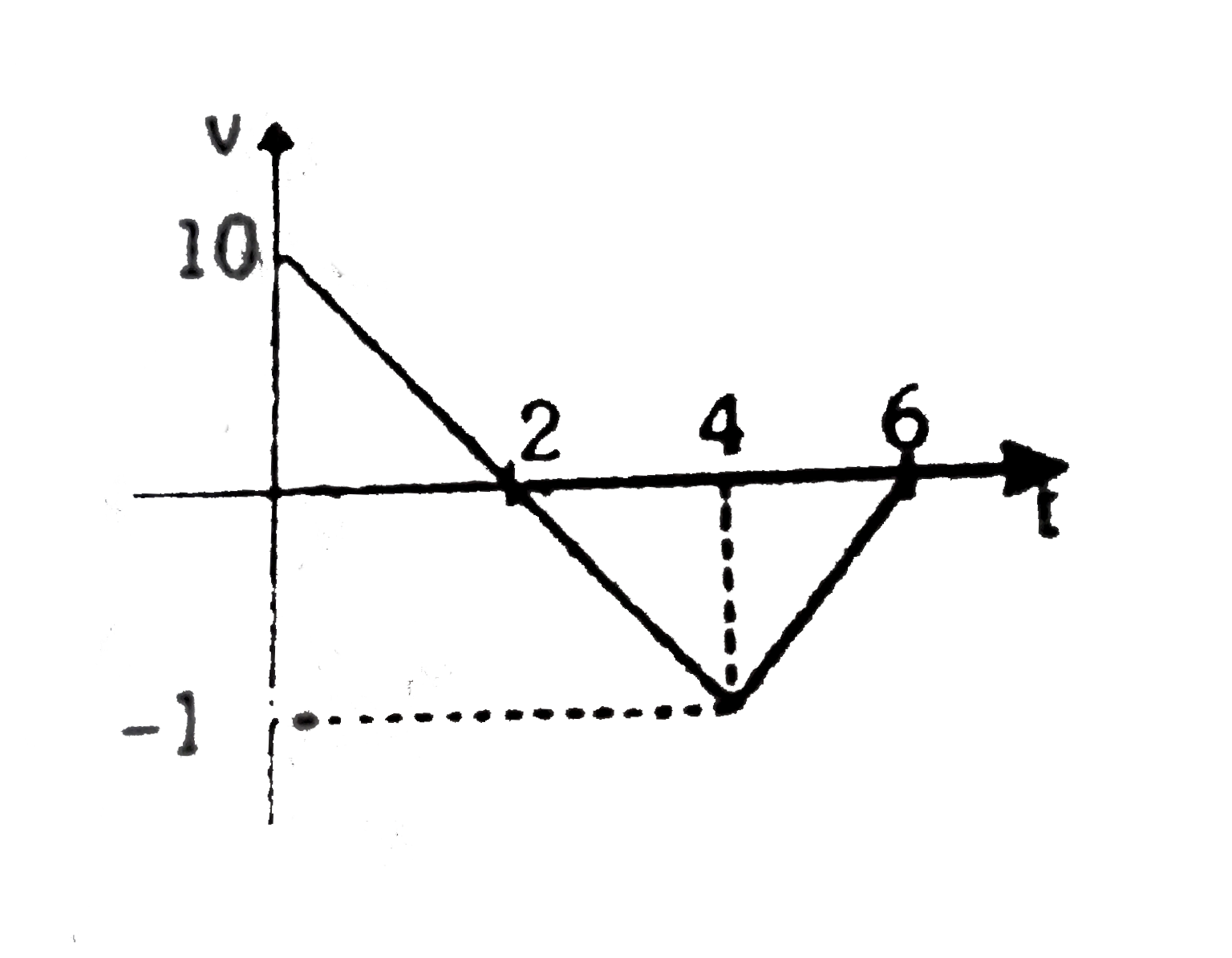
Column IColumn II(A)Change in velocity(p)−5/3SIunit(B)Average acceleration(q)−20SIunit(C)Total displacement(r)−10SIunit(D)Acceleration ay t=3s(s)−5SIunit
View SolutionA balloon rises up with constant net acceleration of 10 m//s^(2) . After 2 s a particle drops from the balloon. After further 2 s match the following : ("Take" g=10 m//s^(2)) {:(,"Column I",,,"Column II"),((A),"Height of perticle from ground",,(p),"Zero"),((B),"Speed of particle",,(q),10 SI "units"),((C),"Displacement of Particle",,(r),40 SI "units"),((D),"Acceleration of particle",,(s),20 SI "units"):}
View Solutionballoon is rising vertically up with a velocity of 29 m/s. A stone is dropped from it and it reaches the ground in 10 seconds. The height of the balloon when the stone was dropped from it is (g = 9.8 m/s^2)
View SolutionIn the diagram shown in figure, match the following columns (take g=10 ms^(-2) ) {:("Column I","Column II"),("(A) Normal reaction","(p) 12 SI unit"),("(B) Force of friction","(q) 20 SI unit"),("(C) Acceleration of block","(r) zero"),(,"(s) 2 SI unit"):}
View Solutionत्वरण का S.I. मात्रक मीटर/सेकण्ड है ।
View SolutionA balloon starts rising from the ground with an acceleration of 1.25 m/s2. A stone is released from the balloon after 10s. Determine
(i) maximum height of stone from the ground.
(ii) time taken by stone to reach the ground.
(Assume, g = 10 m/s2)
View SolutionA particle is relased from a height 20 m from the ground . After how much time and with what speed the particle hits time and with what speed the particle hits the ground ?
[Take :g=10m⋅s−2]
View SolutionA balloon starts rising from thee ground with an acceleration of 1.25 m//s^(2) . After 8 s, a stone is released from the balloon. The stone will (taking g = 10 ms^(-2) )
View SolutionThe particle is executing "SHM" with acceleration 64times10^(-2)m/s^(2) and displacement 4times10^(-2)m .Then the time period is (A) 10s (B) (pi)/(2)s (C) (pi)/(10)s (D) (1)/(10)s
View Solution
