A projectile is launched at an angle α from a cliff of height H above the sea level. If it falls into the sea at a distance D from the base of the cliff, show that its maximum height above the sea level is
[H+D2tan2α4(H+Dtanα)]Solution in Gujrati
ucosαt=D …(i)
ucosαt−12gt2=−H …(ii)
⇒t=2usinα±√u2sin2α+2gHg=Ducosα
h=(usinα)22g=D2tan2α4(H+Dtanα)
∴Hmax=h+H=H+D2tan2α4(H+Dtanα)

Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Exercise-05 [A]11videos
KINEMATICS
- BOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Exercise-05[B]5videos
KINEMATICS
- BOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-04[A]35videos
KINEMATICS
- BOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
Similar Questions
A ball whose kinetic energy is E , is projected at an angle of 45∘ to the horizontal . The kinetic energy of the ball at the highest point of its flight will be
06:33View SolutionA particle goes from point A and B, moving in a semcircle of raidus 1.0m, in 1.0 s, as shown in the figure. The magnitude of the average velocity of the particle is
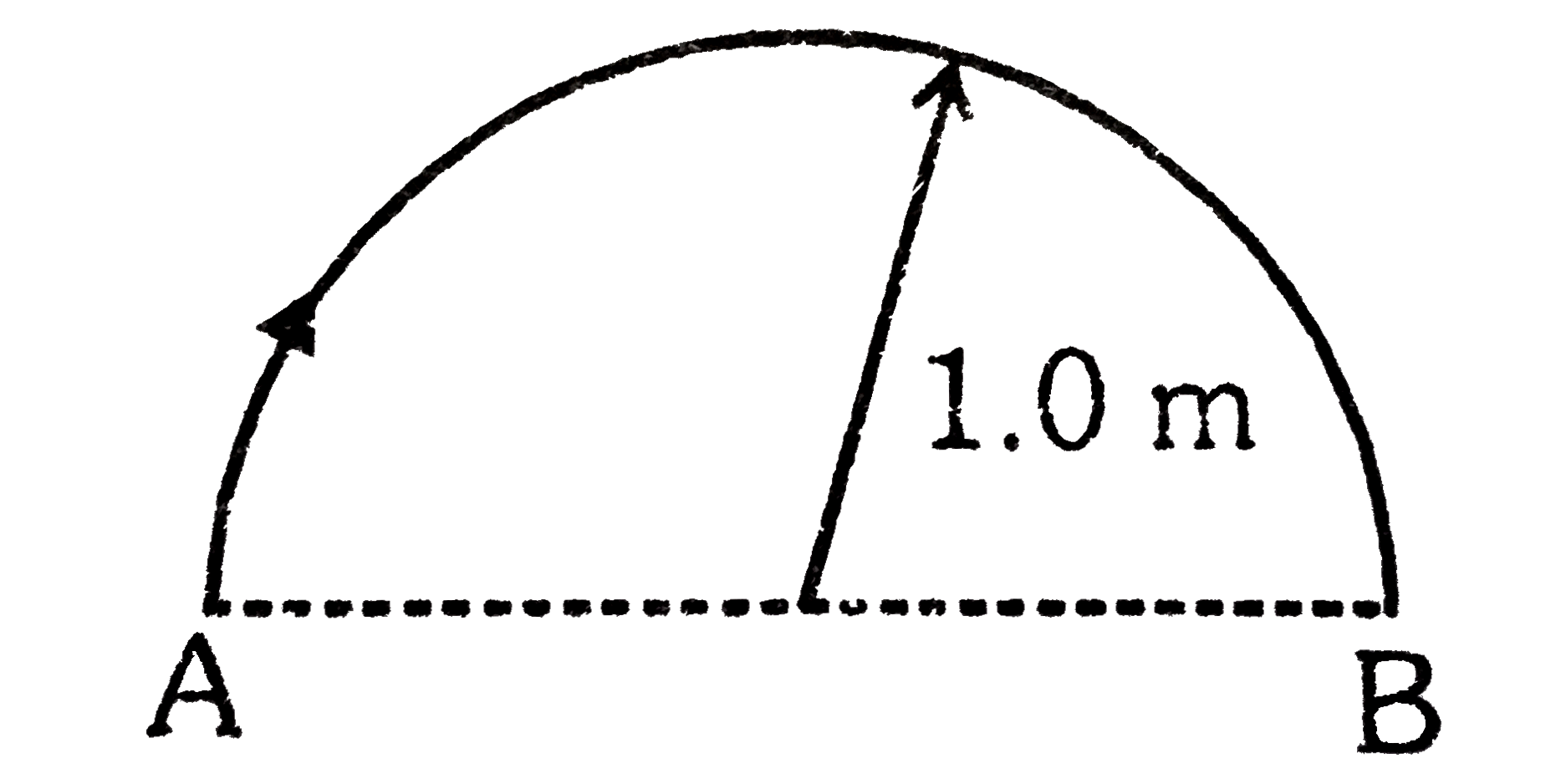 06:32View Solution
06:32View SolutionFig. 2 (NCT).9 show the x−t plot of a particle in one dimensional motion. Three different equal intervals of time are shown. In which interval the average speed is greatest and in which it is the least ? Give th sign of average speed for each interval.
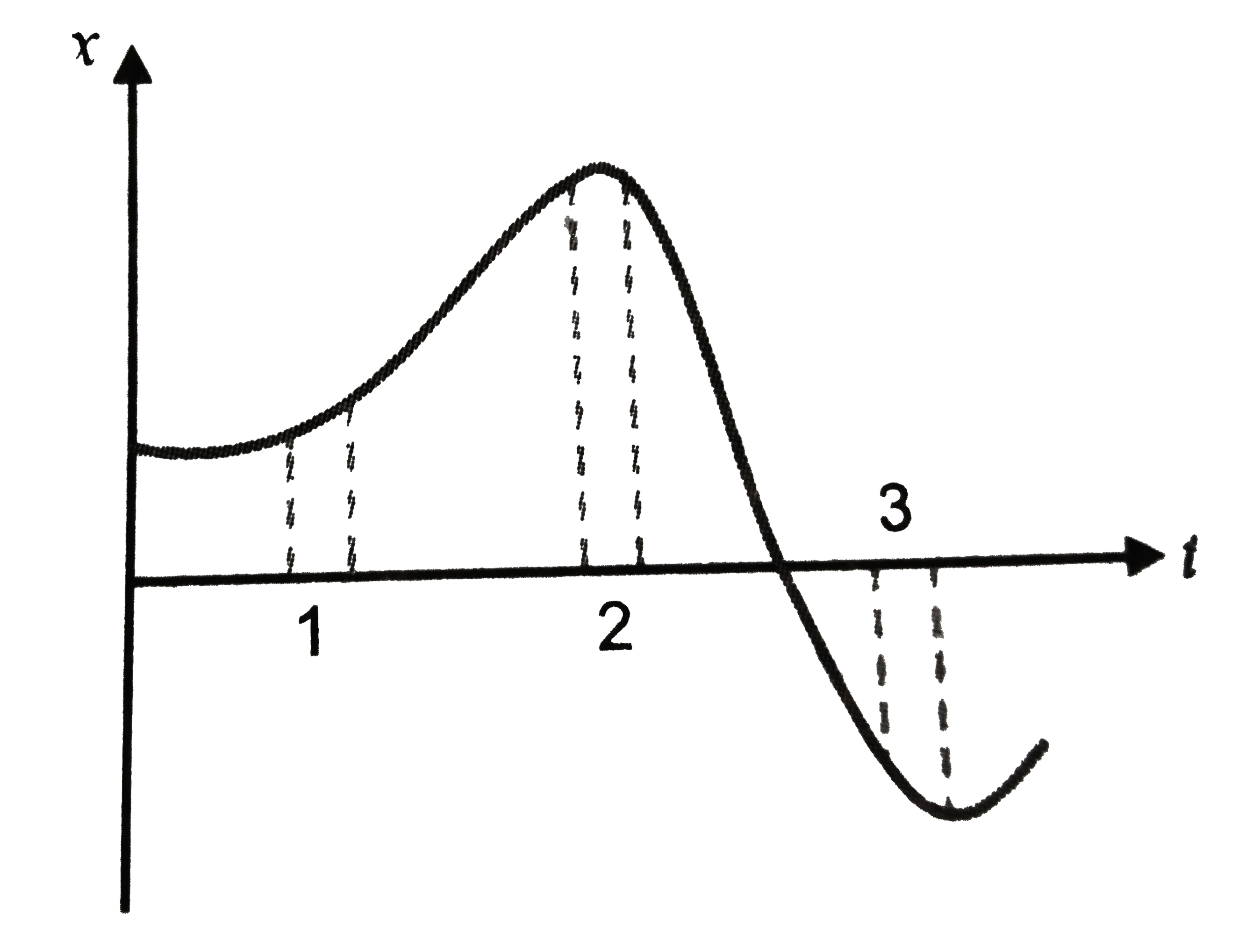 .05:30View Solution
.05:30View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
01:49View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
03:03View SolutionThe angle of elevation of a stationary helicopter as seen from a point on the deck of a ship 60m above sea level,is 30^(@) and the angle of depression of its reflection in the water is 60^(@). Find the height of the helicopter above the sea-level.
03:31View SolutionIf the angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the take is β , prove that the height of the cloud is h(tanβ+tanα)tanβ−tanα
06:34View SolutionThe angles of elevation of a cliff at a point A on the ground and at a point B100mt vertically above A are alpha are beta respectively.The height of the cliff in metres is
03:37View SolutionA stone is projected at an angle alpha to the horizontal from the top of a tower of height 3h. If the stone reaches a maximum height 'h', above the tower, show that it reaches the ground at a distance 6h cot alpha from the foot of the lower.
View SolutionProve that for a projectile fired from level ground at an angle θ above the horizontal, the ratio of the maximum height H to the range R is given by
HR=14tanθ04:26View Solutionएक झील से h मीटर ऊँचाई पर बादलों का उन्नयन कोण α है तथा झील में उसकी परछाई का अवनमन कोण β है। सिद्ध कीजिए की बादलों की ऊंचाई h(tanβ+tanα)tanβ−tanα है।
View Solutionएक व्यक्ति समुद्री के डेक पर समुद्र तल से 10 मीटर की ऊँचाई पर है | वह एक स्तम्भ के शीर्ष का उन्नयन कोण 45∘ तथा उसके आधार का अवनमन कोण 30∘मापता है | स्तम्भ की जहाज से दूरी तथा उसकी ऊँचाई ज्ञात कीजिए |
06:35View SolutionIf asecα−ctanα=d and bsecα+dtanα=c, then eliminate α from above equations.
07:44View SolutionShow that the volume of the greatest cylinder which can be inscribed in a cone of height h and semi - vertical angle α is 427πh3tan2α . Also show that the height of the cylinder is h3 .
08:43View SolutionAn observer on the top of a cliff 200 m above the sea level, observes the angles of depression of two ships on opposite sides of the cliff to be 45∘and30∘ respectively. Then the distance between the ships if the line joining the points to the base of the cliff
01:41View SolutionA large tan filled with water to a height ''h'' is to be emptied through a small hole at the bottom. The ratio of the time taken for the level to fall from h to h/2 and that taken for the level to fall from h/2 to 0 is
01:14View Solution

