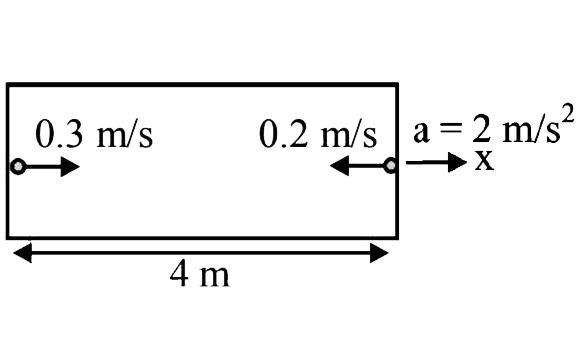
A rocket is moving in a gravity free space with a constant acceleration of 2m/s2 along +x direction (see figure). The length of a chamber inside the rocket is 4m. A ball is thrown from the left end of the chamber in +x direction with a speed of 0.3m/s relative to the rocket . At the same time , another ball is thrown in +x direction with a speed of 0.2m/s drom its right end relative to the rocket . The time in seconds when the two balls hit each other is
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:8 or 2
Assuming open chamber

Vrelative=0.5m/s
Srelative=4m
time =40.5=8m/s
Alternate
Assuming closed chamber
In the frame of of chamber:

Maximum displacement of ball A from its left end is
u2A2a=(0.3)22(2)=0.0225m
This is negligible with respect to the length of chamber i.e. 4m. So, the collision will be very close to the left end.
Hence, time taken by ball B to reach left end will be given by
S=uBt+12at2
4=(0.2)(t)+12(2)(t)2
Solving this, we get
t≈2s
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - PHY
60 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-1
75 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - SUBJECTIVE QUESTION
3 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
Position vector →r of a particle varies with time t accordin to the law →r=(12t2)ˆi−(43t1.5)ˆj+(2t)ˆk, where r is in meters and t is in seconds. Find suitable expression for its velocity and acceleration as function of time.
View SolutionA stone tied to the end of a string 0.4 m long is whirled in a horizontal circle with a constant speed. If the stone makes 10 revolutions in 25 s, the magnitude of acceleration is :
View SolutionA large heavy box is sliding without friction down a smooth plane of inclination θ. From a point P on the bottom of the box, a particle is projected inside the box. The initial speed of the particle with respect to box is u and the direction of projection makes an angle α with the bottom as shown in figure.

(i) Find the distance along the bottom of the box between the point of projection P and the point Q where the particle lands. (Assume that the particle does not hit any other surface of the box. Neglect air resistance).
(ii) If the horizontal displacement of the particle as seen by an observer on the ground is zero, find the speed of the box with respect to the ground at the instant when the particle was projected.
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionThe rate of mass of the gas emitted from the rear of a rocket is initially 0.1kg/s. If the speed of the gas relative to the rocket is 50m/s and the mass of the rocket is 2kg , then the acceleration of the rocket in m/s2 is
View SolutionThe mass of a rocket is 500 kg and the relative velocity of the gases ejecting from it is 250 m/s with respect to the rocket. The rate of burning of the fuel in order to give the rocket an initial acceleration 20m/s2 in the vertically upward direction g=10ms2, will be -
View SolutionA rocket is moving in a gravity free space with a constant acceleration of 2ms^(-1) along +x direction (see Fig.5.126). The length of a chamber inside the rocket is 4m. A ball is thrown from the left end of the chamber in +x direction with a speed of 0.3 ms^(-1) relative to the rocket. At the same time , another ball is thrown in -x direction with a speed of 0.2ms^(-1) from its right and relative to the rocket. the time in seconds when the two balls hit each other is:
View SolutionA rocket of mass 120kg. Is fired in the gravity free space is ejected gases with velocity 600 m/s at the rate of 1kg/s. what will be the initial accleration of the rocket:-
View SolutionIf rocket engine ejects fuel at the rate μ kg/s with relative velocity vr. At time t = 0, speed of rocket is u. Consider the value of acceleration due to gravity is constant and equal to g.
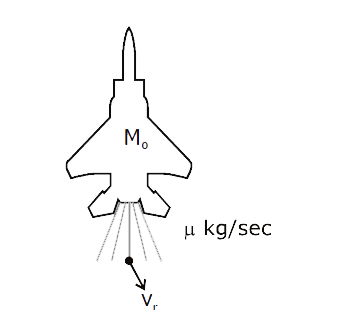
If rocket is in gravity free space then find velocity of rocket as function of time.
View Solutionएक रॉकेट गुरुत्वहीन अंतरिक्ष में नियत त्वरण 2 मी/से2 से +x दिशा में गतिमान है। रॉकेट के कक्ष की बाई दीवार से एक गेंद रॉकेट के सापेक्ष 0.3मी/से की गति से +x दिशा के अनुदिश फेंकी जाती है । ठीक उसी समय एक दूसरी गेंद की दाईं दीवार से रॉकेट के सापेक्ष 0.2मी/से की गति से +x दिशा के अनुदिश फेंकी जाती है। दोनों गेंदों के एक-दूसरे से टकराने तक लगने वाला समय सेकंड में है।

View SolutionIf M is the mass of the rocket, r is the rate of release of gases relative to the rocket, then the acceleration of the rocket (dv)/(dt) (Gases move relative to rockets = u)
View Solutiont = 0 पर एक रॉकेट पृथ्वी की सतह से ऊर्ध्वाधर ऊपर की ओर 9.8 मी/से2 त्वरण से गति करना प्रारम्भ करता है। t = 0 पर ही रोकेट के सापेक्ष शून्य चाल से एक प्रेक्षेप्य को रॉकेट से छोड़ा जाता है। प्रक्षेप्य का त्वरण होगा (g = 9.8 मी/से2)
View SolutionA ball reaches a rocket at 60 m/s along + X direction, and leaves the rocket in the opposite direction with the same speed. Assuming that the mass of the ball as 50gm and the contact time is 0.02 second, the force exerted by the racket on the ball is
View Solution120 kg के रॉकेट को गुरूत्वहीन अन्तरिक्ष में छोड़ने पर रॉकेट से 600 m/s के वेग से तथा 1 kg/s की दर से गैस बाहर निकलती है, तो रॉकेट का प्रारम्भिक त्वरण है :
View SolutionThe driver of a car moving towards a rocket launching pad with a speed of 6 m s^(-1) observed that the rocket is moving with speed of 10 m s^(-1) . The upward speed of the rocket as seen by the stationery observer is nearly
View Solution
