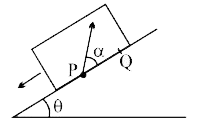
A large heavy box is sliding without friction down a smooth plane of inclination θ. From a point P on the bottom of the box, a particle is projected inside the box. The initial speed of the particle with respect to box is u and the direction of projection makes an angle α with the bottom as shown in figure.

(i) Find the distance along the bottom of the box between the point of projection P and the point Q where the particle lands. (Assume that the particle does not hit any other surface of the box. Neglect air resistance).
(ii) If the horizontal displacement of the particle as seen by an observer on the ground is zero, find the speed of the box with respect to the ground at the instant when the particle was projected.Solution in Gujrati
The correct Answer is:(i) u2sin2αgcosθ (ii) v=ucos(α+θ)cosθ
(i) u is the relative velocity of the particle with respect to the box.

ux is the relative velocity of particle with respect to the box in x-direction. uy is the relative velocity with respect to the box in y-direction. Since there is no velocity of the box in the y-direction, therefore this is the vertical velocity of the particle with respect to ground also.
Y-direction motion
(Taking relative terms w.r.t. bx)
uy=+usinα,ay=−gcosθ
s=ut+12at2⇒0=(usinα)t−12gcosθ×t2
⇒t=0 or t=2usinαgcosθ
X-direction motion
(taking relative terms w.r.t. box)
ux=+ucosα & s=ut+12at2
ax=0⇒sx=ucosα×2usinαgcosθ=u2sin2αgcosθ
(ii) for the observer (on ground) to see the horizontal displacement to be zero, the distance travelled by the box in time (2usinαgcosθ) should be equal to the range of the particle. Let the speed of the box at the time of projection of particle be u. Then for the motion of box with respect to ground.
ux=−v,s=vt+12at∘,ax=−gsinθ
sx=−u2sin2αgcosθ=−c(2usinαgcosθ)−12gsinθ(2usinαgcosθ)2
On solving we get v=ucos(α+θ)cosθ
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Integer Type Question
3 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - PHY
60 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - MCQ with one or more than one correct Question
1 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A train is moving along a straight line with a constant acceleration 'a' . A boy standing in the train throws a ball forward with a speed of 10m/s, at an angle of 60(∘) to the horizontal. The boy has to move forward by 1.15m inside the train to catch the ball back at the initial height . the acceleration of the train , in m/s2 , is
View SolutionPosition vector →r of a particle varies with time t accordin to the law →r=(12t2)ˆi−(43t1.5)ˆj+(2t)ˆk, where r is in meters and t is in seconds. Find suitable expression for its velocity and acceleration as function of time.
View SolutionThe coordinate of a particle moving in a plane are given by x(t)=acos(pt)andy(t)=bsin(pt) where a,b(<a) and P are positive constants of appropriate dimensions . Then
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

View SolutionA box is falling freely. Inside the box, a particle is projected with some velocity v with respect to the box at an angle theta as shown in the figure. Assertion (A) : The path of the particle with respect to an oberver sitting in the box will be a straight line. Reasoning (R ) : The acceleration of particle with respect to the box is zero. Then,
View SolutionA rectangular box is sliding on a smooth inclined plane of inclination theta . At t=0 the box starts to move on the inclined plane. A bolt starts to fall from point A . Find the time after which bolt strikes the bottom surface of the box.
View SolutionA box is failing freely. Inside the box, a particle is projected with some velocity v with respect to the box at an angle θ as shown in the figure.

View SolutionA very heavy box is kept on a frictionless incline plane inclined at an angle θ from the horizontal. Box is having an another frictionless incline plane, inclined plane as shown in the figure. A block of mass m is kept on this inclined plane inside the box. Acceleration of block w.r.t. box is
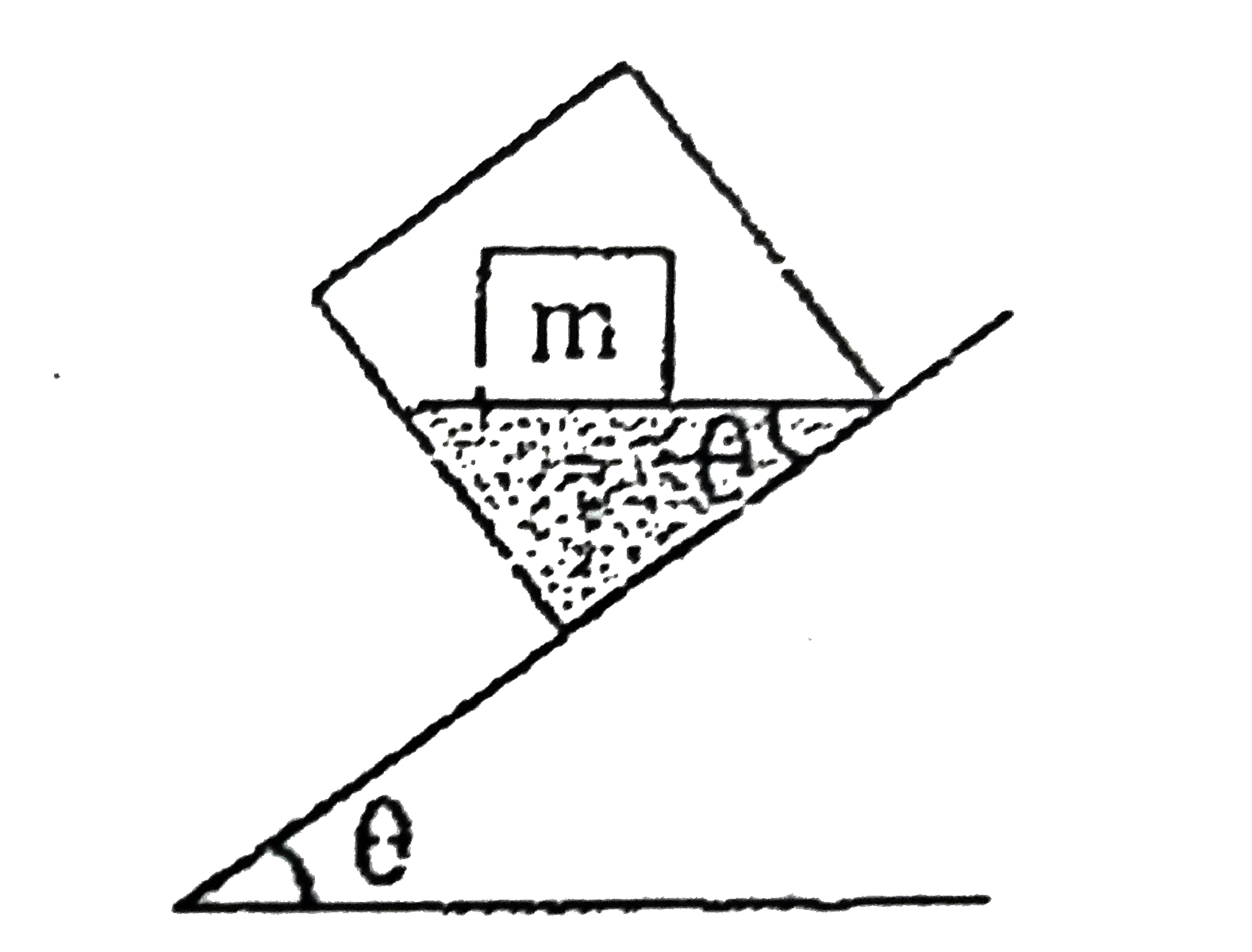
View SolutionA large box is moving on a horizontal floor with constant acceleration a=g. A particle is projected inside box with velocity u and angle theta with horizontal from box frame. For the given u, the value of theta for which horizontal range inside he box will be maximum is
View SolutionA rectangular box lies on a rough inclined surface. The coefficient of friction between the surface and the box is (μ) Let the mass of the box be m.
At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane ?
View SolutionA box is lying on an inclined plane if the box slides when the angle of inclination is 60^(@) then the coefficient of static friction of the box and the plane is?
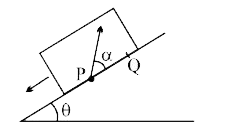
View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

View Solutionθ नत कोण वाले घर्षण रहित तल पर एक बड़ा भारी बॉक्स फिसल रहा है। बाक्स के तल पर स्थित बिन्दु P से बॉक्स के भीतर एक कण प्रक्षेपित किया जाता है। कण की बॉक्स के सापेक्ष प्रारम्भिक वेग u है तथा प्रक्षेपण की दिशा तल से चित्रानुसार α है।
(a) बॉक्स में नत के अनुदशि प्रक्षेपण बिन्दु P से Q की दूरी ज्ञात करो जहाँ कण टकराता है। (कण बॉक्स में और कही नही टकराता एवं वायु प्रतिरोध नगण्य है
View Solutionθ नत कोण वाले घर्षण रहित तल पर एक बड़ा भारी बॉक्स फिसल रहा है। बाक्स के तल पर स्थित बिन्दु P से बॉक्स के भीतर एक कण प्रक्षेपित किया जाता है। कण की बॉक्स के सापेक्ष प्रारम्भिक वेग u है तथा प्रक्षेपण की दिशा तल से चित्रानुसार α है।
यदि धरातल पर खड़े प्रेक्षक के लिये कण का क्षैतिज विस्थापन शून्य हो तो जब कण प्रक्षेपित किया गया था तब बॉक्स की धरातल के सापेक्ष चाल क्या थी।
View Solution
