A particle of mass m rests on a horizontal floor with which it has a coefficient of static friction $μ$ . It is desired to make the body move by applying the minimum possible force F. Find the magnitude of F and the direction in which it has to be applied.Solution in Gujrati

A

${tan}^{- 1} μ, \frac{μ m g}{\sqrt{(1 + μ^{2})}}$

B

${tan}^{- 1} μ, \frac{m g}{\sqrt{(1 + μ^{2})}}$

C

${tan}^{- 1} μ, \frac{μ m g}{\sqrt{(1 - μ^{2})}}$

D

${tan}^{- 1} μ, \frac{m g}{\sqrt{1 - μ^{2}}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

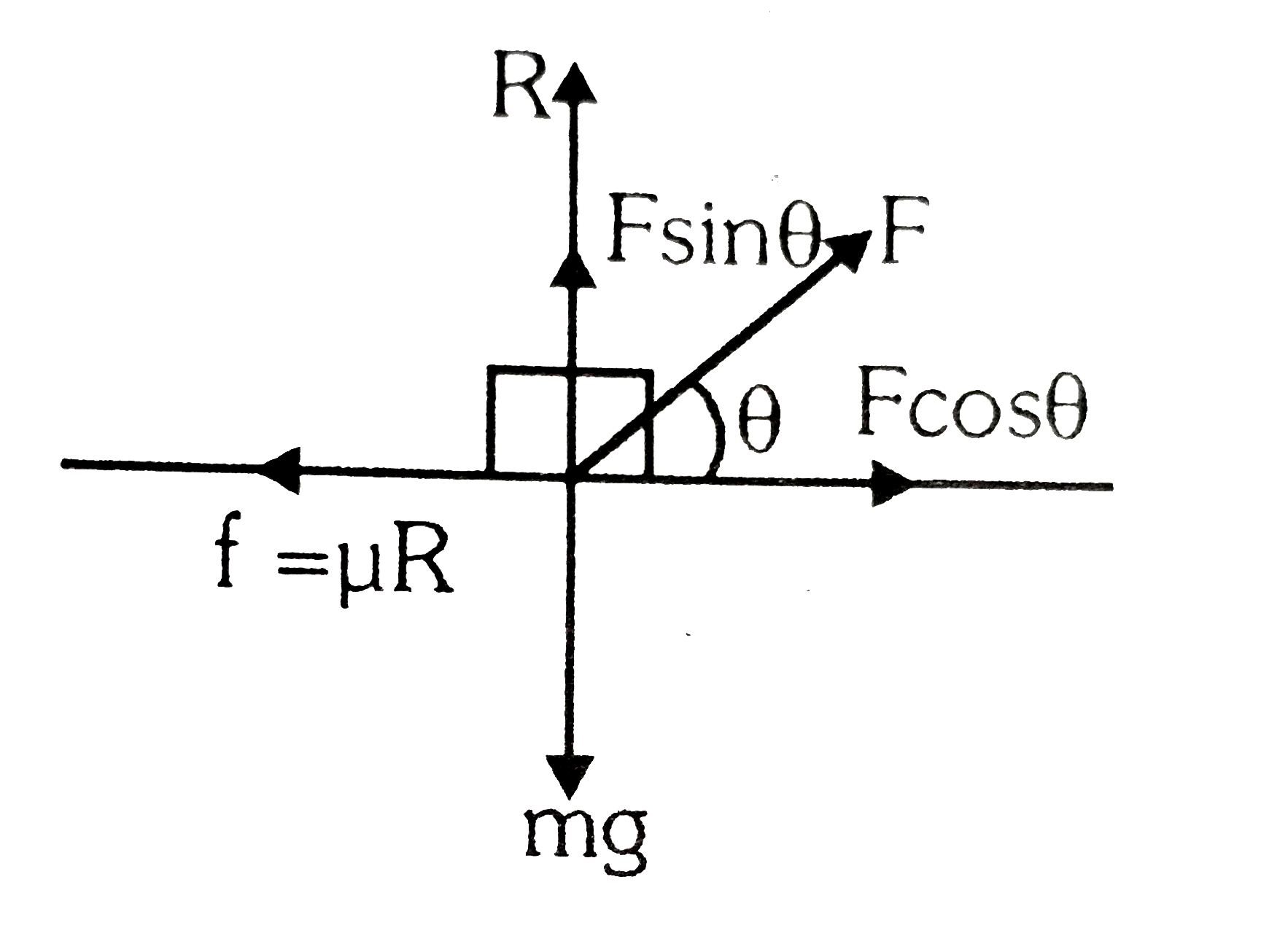
$R = F sin θ = m g$
$R = m g - F sin θ$
Force of friction, $f = μ R = μ (m g - F sin θ)$
The block will move, when
$F cos \geq f$
$F cos θ \geq μ (m g - sin θ)$
$F \geq \frac{μ m g}{cos θ + μ sin θ}$ ....(i)
F will be minimum, when
$cos θ + μ sin θ =$ maximum , for which
$\frac{d}{d θ} (cos θ + μ sin θ) = 0$
or $- sin θ + μ cos θ = 0$ or $μ cos θ = sin θ$
or $tan θ = μ$ or $θ = {tan}^{- 1} (μ)$
$∴ sin θ = \frac{μ}{\sqrt{1 + μ^{2}}}$ and $cos θ = \frac{1}{\sqrt{1 + μ^{2}}}$
From (ii),
$F \geq \frac{μ m g}{\frac{1}{\sqrt{1 + μ^{2}}} + \frac{μ^{2}}{\sqrt{1 +_{μ}^{2}}}}$
$F \geq \frac{μ m g}{\sqrt{1 + μ^{2}}} ∴ F_{min} = \frac{μ m g}{\sqrt{1 + μ^{2}}}$

|

Class 12 PHYSICS NEWTONS LAWS OF MOTION

Topper's Solved these Questions

Similar Questions

ALLEN -NEWTONS LAWS OF MOTION-EXERCISE-I

Home
Ask Doubt
Profile