[Gujrati] A piece of wire is bent in the shape of a parabola y=kx^(2)

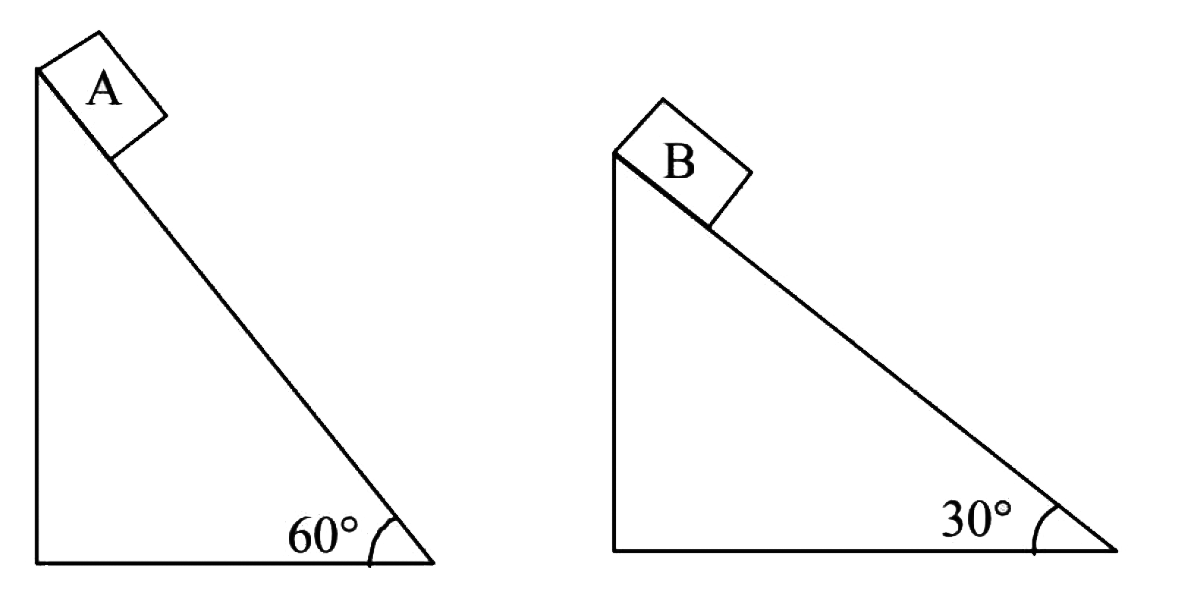
Two fixed frictionless inclined planes making an angle $30^{\circ}$ and $60^{\circ}$ with the vertical are shown in figure. Two blocks A and B are planes. What is the relative vertical acceleration of A with respect to B?
ocr_image

View Solution

A particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If $α and β$ are the base angles of triangle and angle of projection is $θ$ , then prove that $(tan θ = tan α + tan β)$

View Solution

Assertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.

View Solution

A piece of wire is bent in the shape of a parabola y = Kx^(2) (y - axis vorical) with a bead of mass m on it . The beat can side on the wire without friction , it stays the wire is now accleated parallel to the bead , where the bead can stay at rest with repect to the wire from the y - axis is

View Solution

A bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is $x^{2} = 4 a y$ . The wire frame is fixed and the bead is released from the point $y = 4 a$ on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by $y = a$ is
ocr_image

View Solution

A piece of wire is bent in the shape of a parabola $y = k x^{2}$ (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:

View Solution

एक तार के टुकड़े को परवलय $y = k x^{2}$ (Y-अक्ष ऊर्ध्वाधर ) आकर में मोड़ा गया है तार में m द्रव्यमान का एक मनका पड़ा है जो तार पर बिना घर्षण सरक सकता है तार की स्थिर अवस्था में यह मनका परवलय के निम्नतम बिंदु पर रहता है अब तार को एकसमान त्वरण a से X- अक्ष के समान्तर चलाया जाता है मनके की नई साम्यावस्था में , जहाँ वह तार की अपेक्षा स्थिर अवस्था में रह सकता है Y-अक्ष से दूरी होगी

View Solution

A piece of wire is bent in the shape of a parabola $y = k x^{2}$ (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?

View Solution

A piece of wire is bent in the shape of a parabola $y = k x^{2}$ (y-axis vertical) with a bead of mass 'm' on it. The bead can slide on the wire without friction. The wire is now accelerated parallel to the x-axis where the with an acceleration'a'. The distance of the new equilibrium position of the bead is $\frac{a}{x g k}$ where the bead can stay at rest with respect to the wire from y-axis. The value of x' is

View Solution

A piece of wire is bent in the shape of a parabola y = kx^2 (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?

View Solution

A piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:

View Solution

A piece of wire is bent in the shape of a parabola y=kx^(2) (yaxis vertical ) with a bead of mass m on it . The bead can slide on the wire without friction . It stays at the lowest pint of the parabola when the wire is at rest.The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead. Find the X-coordinate where the bead can stay at rest with respect to the wire?

View Solution

Parabola to a piece of string y = kx^(2) (y-axis vertical) is folded into a shape above which a bead of m mass, the bead can slip without friction. When the wire is stationary, the bead is at its minimum point. The parallel is accelerated. From the y axis in the position of pearl equinox x_(0) At a distance where the pearl is at rest with respect to the wire x_(0) What will be the value of?

View Solution

चित्रानुसार परवलय की समीकरण $x^{2} = 4$ ay है । इसकी ऊर्ध्वाधर अक्ष तथा शीर्ष मूल बिंदु पर है, इस परवलय तार पर m द्रव्यमान की मनका स्थित है। तार का फ्रेम स्थिर एवं ऊर्ध्वाधर तल में है तथा मनका (मनका) बिना घर्षण के परवलय पर फिसल सकता है। तार फ्रेम पर y=4a बिंदु से मनका स्थिरावस्था से छोड़ा जाता है। जब मनका y=a स्थिति पर पहुंचता है तो इसका स्पर्शरेखीय त्वरण है:
ocr_image

View Solution

A bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is $x^{2} = 4 a y$ . The wire frame is fixed and the bead is released from the point $y = 4 a$ on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by $y = a$ is
ocr_image

View Solution

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

ALLEN -NEWTON'S LAWS OF MOTION & FRICTION-EXERCISE (JA)