A block slides down a rough inclined plane of slope angle θ with a constnat velocity. It is then projected up the same plane with an intial velocity v the distance travelled by the block up the plane coming to rest is .Solution in Gujrati
v202gsinθ
v204gsinθ
v20sin2θ2g
v20sin2θ4g
The correct Answer is:B
mgsinθ=μmgcosθ
when pushed up
deacc =gsinθ+μgcosθ
∴v2−v20=2(a)×s
∴s=v202(2gsinθ)
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
Similar Questions
Assertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
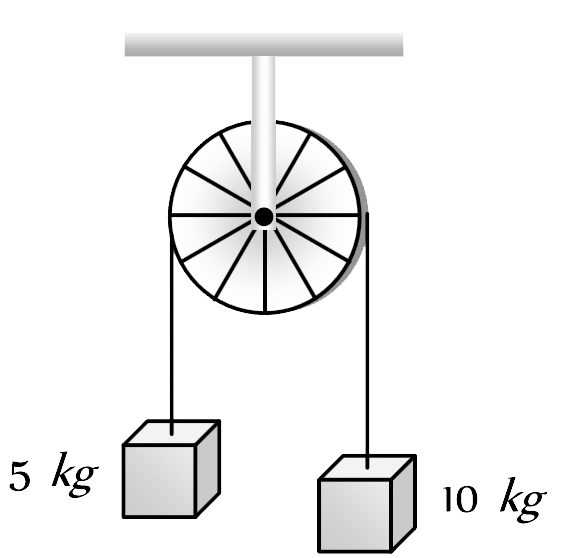
View SolutionUSS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View Solution(a) A block slides down an incline of angle 45^(@) with an acceleration (g)/(2 sqrt(2)) . Find the friction coefficient. (b) A block slides down at 45^(@) inclined plane in twice the time it takes to slide down a smooth 45^(@) incline. What is friction co-efficient between the block and the incline? ( c) A block slides down on a rough inclined plane of inclination 30^(@) with constant velocity. If this block is projected up the plane with a velocity of 10 m//s , then at what distance along the inclined plane , the block will come to rest? (d) A body is launched up on a rough inclined plane of inclination theta . If time of ascent is half of time of descent, find the friction coefficient.
View SolutionA block is released from the top of an inclined plane of inclination theta . Its velocity at the bottom of plane is v . If it slides down a rough inclined plane of the same inclination , its velocity at bottom is v//2 . The coefficient of friction is
View SolutionA block slides down an inclined plane of slope θ with constant velocity. It is then projected up the plane with an initial speed u. How far up the incline will it move before coming to rest ? Will its slide down again ?
View SolutionA block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination theta of the plane to the horizontal will the block just start to slide down the plane?
View SolutionA block can slides down an inclined plane of slope and theta , with constant velocity. If it is projected up the same plane with an initial speed v_(0) , then
View SolutionA block slides down an inclined plane of angle 53∘ with constant velocity .It is then projected up the same plane with an initial velocity of 8m/s . How far up (in m) the inclione will it move before coming to rest?
View SolutionA block slides down a rough inclined plane of slope angle theta with a constant velocity. It is then projected up the same plane with an initial velocity v. The distance travelled by the block up the plane before coming to rest is
View SolutionA block slides down a slope of angle 0 with constant velocity. It is then projected up with a velocity of 10ms^(-1), g=10ms^(-2) & theta = 30°. The maximum distance it can go up the plane before coming to stop is
View SolutionA block is pushed up a rough inclined plane of 45∘ with a velocity u. The block rises up and then comes down sliding to have a velocity u/2 at the bottom. The coefficient of sliding friction between block and the plane is
View SolutionA block slides down a slope of angle theta with constant velocity. It is then projected up with a velocity of 10ms^(-1) g= 10ms^(-2) & theta= 30^(@) . The maximum distance it can go up the plane before coming to stop is
View SolutionA block slides down a slope of angle with constant velocity. It is then projected up with a velocity of 10ms−1,g=10ms−2&θ=30∘. The maximum distance it can go up the plane before coming to stop is
View SolutionA block is pushed up a rough inclined plane of 45∘ with a velocity u. The block rises up and then comes down sliding to have a velocity u/2 at the bottom. The coefficient of sliding friction between block and the plane is
View Solution
