One mole of an ideal monatomic gas undergoes the process P=αT1/2, where α is constant . If molar heat capacity of the gas is βR1 when R = gas constant then find the value of β. Solution in Gujrati
The correct Answer is:2
PαT1/2 and PV=nRt⇒PV−1 = constant ∴C=Cv+R1−(−1)=3R2+R2=2R
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -02
82 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
On an X temperature scale, water freezes at −125.0∘X and boils at 375.0∘X. On a Y temperature scale, water freezes at −70.0∘Y and boils at −30.0∘Y. The value of temperature on X-scale equal to the temperature of 50.0∘Y on Y-scale is
View SolutionA triangular plate has two cavities , one square and one rectangular as shown in figure . The plate is heated.
_E01_066_Q01.png)
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.
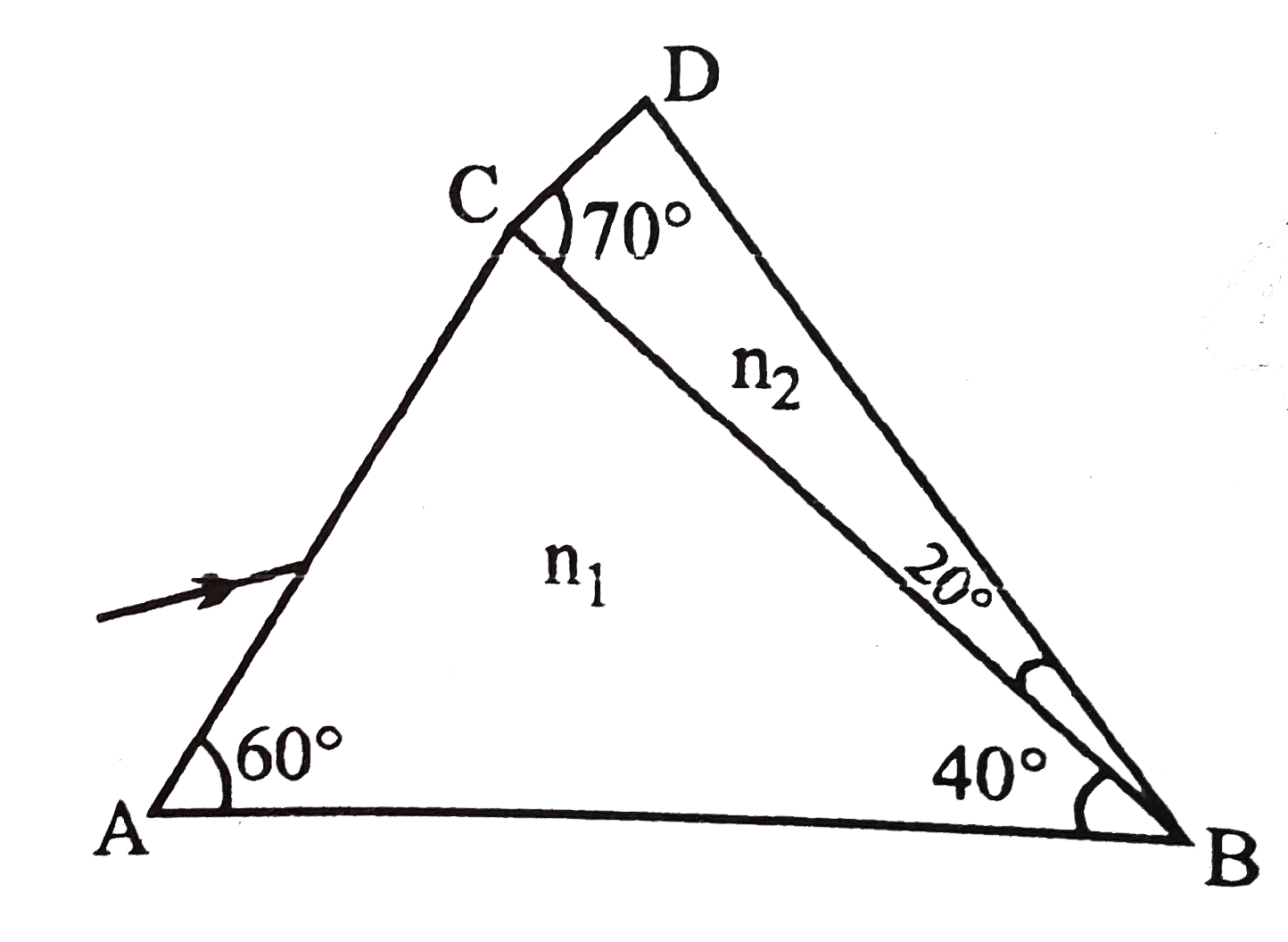
(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionOne mole of an ideal monatomic gas undergoes the process p=αT1/2, where α is a constant.
(a) Find the work done by the gas if its temperature increases by 50K.
(b) Also, find the molar specific heat of the gas.
View SolutionOne mole of an ideal monoatomic gas undergoes a process as shown in the figure. Find the molar specific heat of the gas in the process.
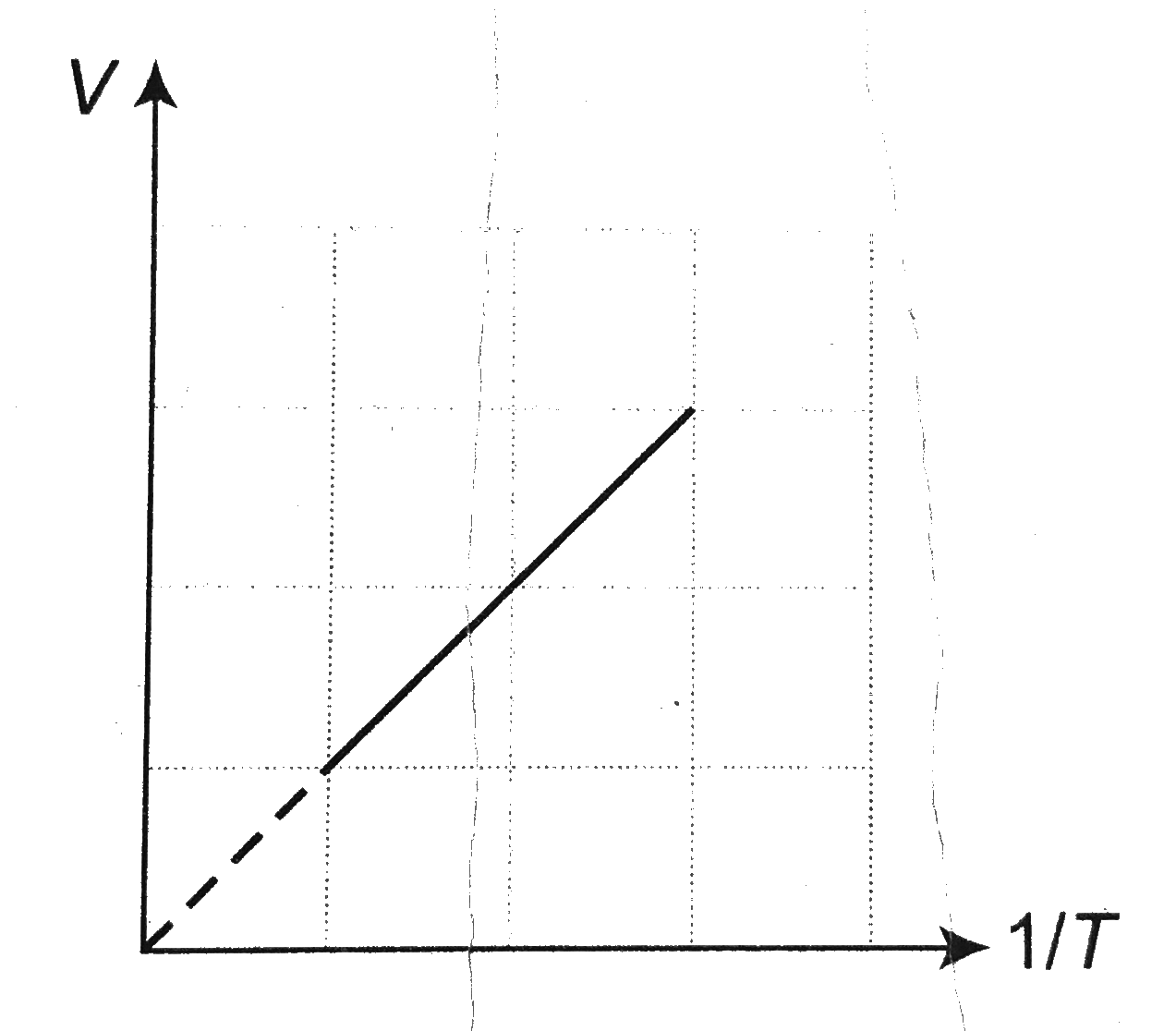
R is a gas constant.
View SolutionOne mole of an ideal monatomic gas undergoes a process described by the equation PV3= constant. The heat capacity of the gas during this process is
View SolutionOne mole of an ideal monatomic gas undergoes the process p=αT1/2 , whwre a is a constant. The work done by the gas if its temperature increases by 50K is 50Rx. Find the value of x.
View SolutionFind the molar heat capacity (in terms of R) of a monoatomic ideal gas undergoing the process: PV1/2=constant?
View SolutionAn ideal gas with heat capacity at constant volume C_(V) undergoes a quasistatic process described by P V^(alpha) in a P-V diagram, where alpha is a constant. The heat capacity of the gas during this process is given by-
View SolutionOne mole of an ideal monatomic gas undergoes a process described by the equation PV3= constant. The heat capacity of the gas during this process is
View SolutionThe heat capacity at constant volume of an ideal gas consisting of monatomic molecules is 3//2 R ( where R is the gas constant ) . The heat capacity at constant pressure is :
View SolutionOne mole of an ideal monatomic gas undergoes a process described by the equation PV^(3) = constant. The heat capacity of the gas during this process is
View SolutionOne mole of an ideal gas undergoes a process such that P∝1√T . The molar heat capacity of this process is 4R, where R is universal gas constant. Then,
View SolutionOne mole of an ideal monoatomic gas undergoes the process P = alpha T^(1//2) where alpha is a constant.
View Solution
