Consider a hypothetical situation where we are comparing the properties of two crystals made of atom A and atom B. Potential energy (U)v/s interatomic separation (r) graph for atom A and atom B is shown in figure (i) and (ii) and respectively.
_E01_204_Q01.png)
It is seen that the potential energy can reach a maximum value of UT at temperature T=10K. if r1 and r2 are 0.9999r0and1.0003r0 for atoms of crystal A, its approximate coefficient of linear expansion can be :-Solution in Gujrati
4×10−5/K
1×10−5/K
2×10−5/K
3×10−5/K
The correct Answer is:C
We have Δravg=(1.0003−0.99992)r0 (from equilibrium position)
∴Δrr0=αΔT⇒α=2×10−5/K
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (A)
48 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)
15 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
40 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Two rods each of length L2 and coefficient of linear expansion α2 each are connected freely to a third rod of length L1 and coefficient of expansion α1 to form an isoscles triangle. The arrangement is supported on a knife-edge at the midpoint of L1 which is horizontal. what relation must exist between L1 and L2 so that the apex of the isoscles triangle is to remain at a constant height from the knife edge as the temperature changes ?
View SolutionThe rectangular box shown in Fig has partition which can slide without friction along the length of the box. Initially each of the two chambers of the box has one mole of a mono-atomic ideal gas (λ=5/3) at a pressure P0, volume V0 and temperature T0. The chamber on the left is slowly heated by an electric heater. The walls of the box and the lead wires of the heater is negligible. The gas in the left chamber expands pushing the partition until the final pressure in both chambers becomes 243P0/32. Determine (i) the final temperature of the gas in each chamber and (ii) the work done by the gas in the right chamber.
View SolutionStatement-1: A real gas behaves as an ideal gas at high temperature and low pressure .
Statement-2: Liquid state of an ideal gas is impossible.
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionThe potential energy function for the force between two atoms in a diatomic molecule is approximate given by U(r)=ar12−br6, where a and b are constants and r is the distance between the atoms. If the dissociation energy of the molecule is D=[U(r=∞)−Uat equilibrium],D is
View SolutionGiven in hydrogen atom r_(n),V_(n),E,K_(n) stand for radius, potential energy, total energy and kinetic energy in n^(th) orbit. Find the value of U,v,x,y. {:((A),u=(V_(n))/(K_(n)),(P),1,),((B),(1)/(r_(n))propE^(x),(Q),-2,),((C),r_(n)propZ^(y),(R),-1,),(,(Z="Atomic number"),,,),((D),v=("Orbital angular momentum of electron"),(S),0,),(,("in its lowest energy"),,,):}
View SolutionThe potential energy between two atoms in a molecule is given by, U(x)=ax12−bx6 , where a and b are positive constant and x is the distance between the atoms. The atoms is an stable equilibrium, when-
View SolutionThe potential energy U of two atoms of a diatomic molecule as a function of distance r between the atoms as shown in the given figure. Read the following statement carefully. 1. The equilibrium separation distance between the atoms is equal to r_(2) . 2. At r = r_(1) , the force between the atom is repulsive. 3. For r gt r_(2) , the force between the atoms is attractive Which of the above statements is true ?
View SolutionConsider a hypothetical situation where we are comparing the properties of two crystals made of atom A and atom B. Potential energy (U)v/s interatomic separation (r) graph for atom A and atom B is shown in figure (i) and (ii) and respectively.
_E01_202_Q01.png)
Choose correct statement
View SolutionConsider a hypothetical situation where we are comparing the properties of two crystals made of atom A and atom B . Potential energy (U) v//s interatomic separation (r) graph for atom A and atom B is shown in figure (i) and (ii) and respectively. When we heat the crystal of either atoms ,the atom undergo oscillation. Choose correct statement for atoms of crystal A
View SolutionIf r is the interatomic distance, a and b are positive constants, U denotes potential energy which is a function dependent on r as follows :
U=ar10−br5.
The equilibrium distance between two atoms is
View SolutionThe potential energy (U) between two atoms in a diatomic molecule as a function of the distance x between atoms has been shown in the adjoining figure. The atoms are
View SolutionThe potential energy of a diatomic molecule is given as U = (a)/(x^(12)) - (b)/(x^(6)) . Find the (i) stable equilibrium distance of separation between two atoms, (ii) force on each atom as the function of separating distance x.
View SolutionThe potential energy U of two atoms of a diatomic molecule as a function of distance r between the atoms as shown in the given figure.
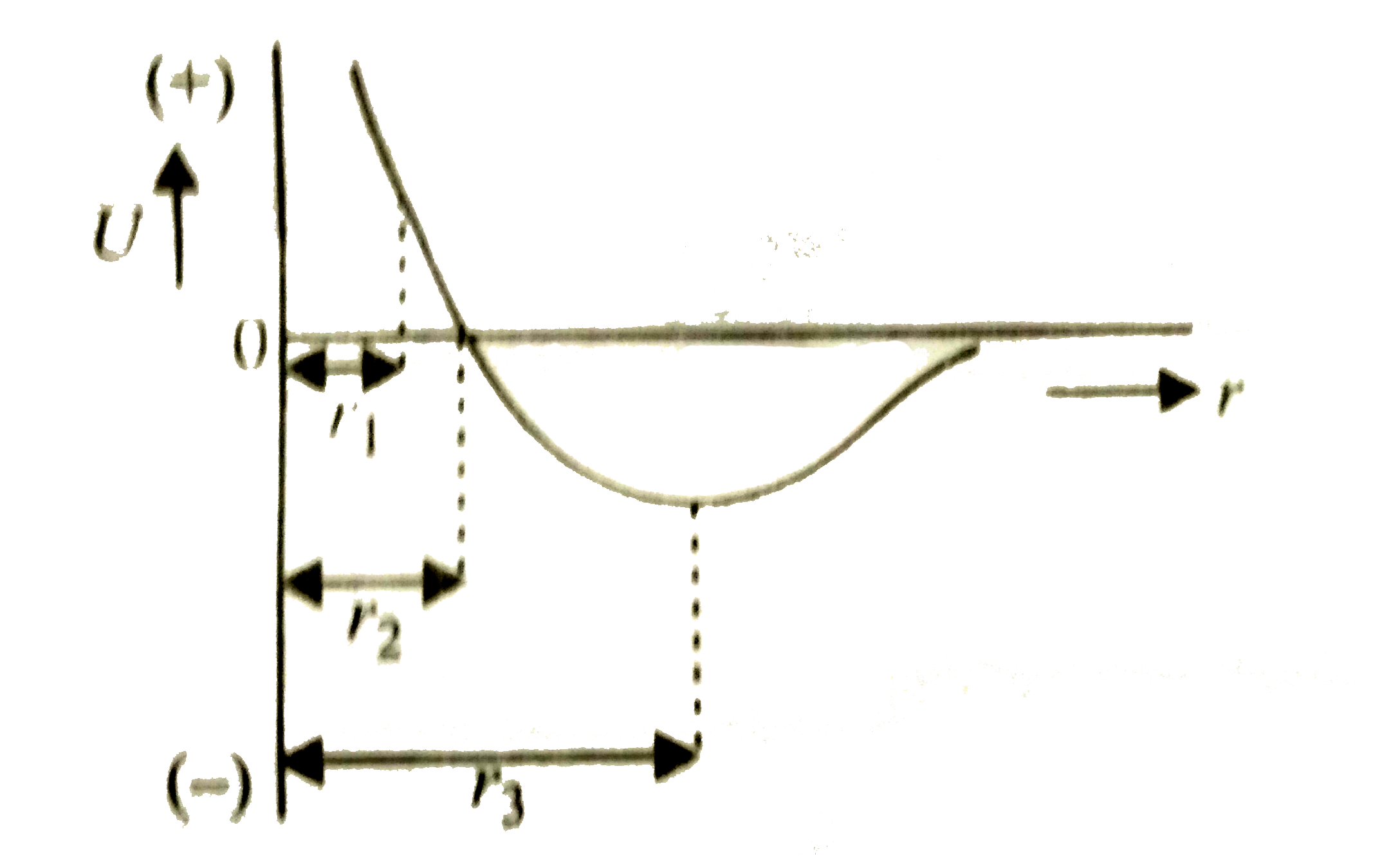
Read the following statement carefully.
1. The equilibrium separation distance between the atoms is equal to r2.
2. At r=r1, the force between the atom is repulsive.
. Forr>r2, the force between the atoms is attractive
Which of the above statements is true ?
View SolutionPotential energy U (for a pair of atoms) versus interatomic separation r for two substance A and B are as shown. For both substance, graphs of U v/s t are on same scale : Where E_(1) , E_(2) and E_(3) are total energy line (for a pair of atoms) and T_(1) , T_(2) and T_(3) are the corresponding temperatures. Also T_(1) gt T_(2) gt T_(3) . {:("Column-I","Column-II"),("A) Expands of heating","P) Substance A"),("B) Contracts on heating","Q) Substance B"),("C) Liquifies above temperature" T_1 ,),("D) Liquifies above temperature" T_2,):}
View Solution
