A small spherical monoatomic ideal gas bubble (γ=5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure P0 (Neglect surface tension).
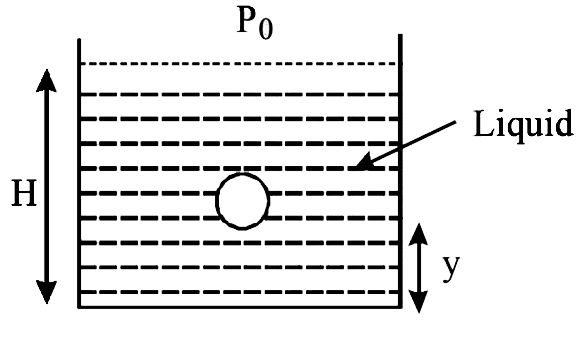
The buoyancy force acting on the gas bubble is (Assume R is the universal gas constant)Solution in Gujrati
plnRgT0(P0+ρlgH)2/5(P0+ρlgy)7/5
plnRgT0(P0+ρlgH)2/5[P0+ρlg(H−y)]3/5
plnRgT0(P0+ρlgH)3/5(P0+ρlgy)8/5
plnRgT0(P0+ρlgH)3/5[P0+ρlg(H−y)]2/5
The correct Answer is:B
Buoyancy force =Vρlg=(nRT2P2)ρlg
=nRρlgT0P0+ρlg(H−y)[P0+ρlg(H−y)P0+ρlgH]25
=ρlnRgT0(P0+ρlgH)25(P0+ρlg(H−y)35)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE- 01
45 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-2
44 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B) (MATCH THE COLUMN)
3 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Two plane mirror M1andM2 are inclined to each other at 70∘. A ray incident on the mirror M1 at an angle θ fallls on M2 and is then reflected parallel to M1 for
View SolutionTwo mirrors are inclined at angle θ as shown in figure. Light rays are incident parallel to one of mirrors. Light will start retracing its path after the reflection if
View SolutionFor the given process :-
_E01_426_Q01.png)
Column-IColumn-II(A)Process J→K(P)W>0(B)Process K→L(q)W<0(C)Process L→M(r)Q>0(D)Process M→J(s)Q<0
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA small spherical monoatomic ideal gas bubble (gamma=5//3) is trapped inside a liquid of density rho (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T_0 , the height of the liquid is H and the atmospheric pressure P_0 (Neglect surface tension). As the bubble moves upwards, besides the buyoncy force the following forces are acting on it
View SolutionA small spherical monoatomic ideal gas bubble (gamma=5//3) is trapped inside a liquid of density rho (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T_0 , the height of the liquid is H and the atmospheric pressure P_0 (Neglect surface tension). When the gas bubble is at a height y from the bottom, its temperature is-
View SolutionA small spherical monoatomic ideal gas bubble (gamma=5//3) is trapped inside a liquid of density rho (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T_0 , the height of the liquid is H and the atmospheric pressure P_0 (Neglect surface tension). The buyoncy force acting on the gas bubble is (Assume R is the universal gas constant)
View SolutionA small spherical monoatomic ideal gas bubble (γ=53) is trapped inside a liquid of density ρl (see figure) . Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure is P0 (Neglect surface tension).
_E01_434_Q01.png)
When the gas bubble is at a height y from the bottom , its temperature is :-
View SolutionA small air bubble of radius r in water is at depth h below the water surface. If P_0 is the atmospheric pressure, rho is the density of water and T is the surface tension of water, what is the pressure inside the bubble?
View Solutionएकपरमाणुक आदर्श गैस का छोटा बुलबुला (γ=53),ρl घनत्व वाले द्रव से घिरा हुआ है। माना कि यह बुलबुला द्रव से किसी प्रकार का ऊष्मीय आदान-प्रदान नहीं करता। बुलबुले में गैस के n मोल है। बुलबुला जब तली में स्थित है तब गैस का ताप T0 है, द्रव स्तम्भ की ऊँचाई H है तथा वायुमंडलीय दाब p0 है (पृष्ठ तनाव नगण्य है)
जैसे-जैसे बुलबुला ऊपर की ओर गति करता है, उत्प्लावन बल के अतिरिक्त जो बल उस पर कार्य करते है,वह है-

View Solutionएकपरमाणुक आदर्श गैस का छोटा बुलबुला (γ=53)ρl घनत्व वाले द्रव से घिरा हुआ है। माना कि यह बुलबुला द्रव से किसी प्रकार का ऊष्मीय आदान-प्रदान नहीं करता। बुलबुले में गैस के n मोल है। बुलबुला जब तली में स्थित है तब गैस का ताप T0 है, द्रव स्तम्भ की ऊँचाई H है तथा वायुमंडलीय दाब p0 है (पृष्ठ तनाव नगण्य है)
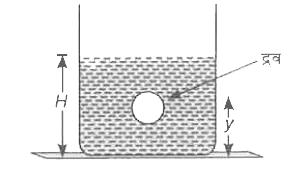
जब बुलबुला बर्तन की तली से y ऊँचाई पर हो, तब उसका ताप होगा
View Solutionएकपरमाणुक आदर्श गैस का छोटा बुलबुला (γ=53)ρl घनत्व वाले द्रव से घिरा हुआ है। माना कि यह बुलबुला द्रव से किसी प्रकार का ऊष्मीय आदान-प्रदान नहीं करता। बुलबुले में गैस के n मोल है। बुलबुला जब तली में स्थित है तब गैस का ताप T0 है, द्रव स्तम्भ की ऊँचाई H है तथा वायुमंडलीय दाब p0 है (पृष्ठ तनाव नगण्य है)
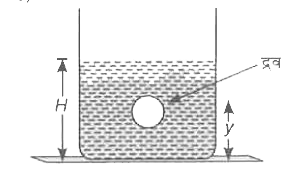
गैस के बुलबुले पर कार्य करने वाला उत्प्लावन बल (R सार्वत्रिक गैस नियतांक है) होगा
View SolutionPassage - II :
A small spherical monoatomic ideal gas bubble (γ−53) is trapped inside a liquid of density ρ1 [ see figure]. Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0. the height of the liquid is H and the atmospheric pressure is ρ0 ( Neglect surface tension)

As the bubble moves upwards, besides the buoyancy force the following forces are acting on it.
View SolutionPassage - II :
A small spherical monoatomic ideal gas bubble (γ−53) is trapped inside a liquid of density ρ1 [ see figure]. Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0. the height of the liquid is H and the atmospheric pressure is ρ0 ( Neglect surface tension)
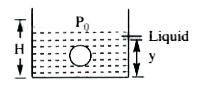
When the gas bubble is at a height y from the bottom, its temperature is :
View SolutionPassage - II :
A small spherical monoatomic ideal gas bubble (γ−53) is trapped inside a liquid of density ρ1 [ see figure]. Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0. the height of the liquid is H and the atmospheric pressure is ρ0 ( Neglect surface tension)

The buoyancy force acting on the gas bubble is :
View Solution
