A fixed thermally conducting cylinder has a radius R and height . The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is .
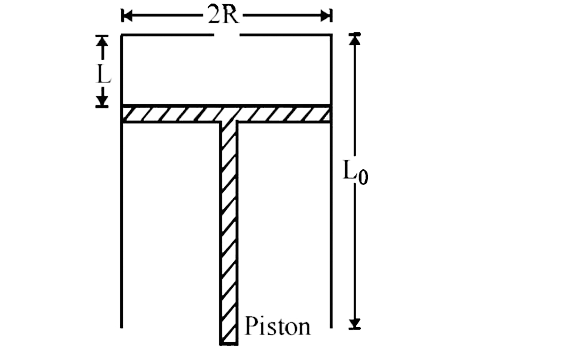
While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top is Solution in Gujrati
The correct Answer is:D
Mg =
Since the cylinder is thermally conducting the temperature remains the same.
_E01_431_S01.png)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE- 01
45 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-2
44 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B) (MATCH THE COLUMN)
3 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Two plane mirror M1andM2 are inclined to each other at 70∘. A ray incident on the mirror M1 at an angle θ fallls on M2 and is then reflected parallel to M1 for
View SolutionTwo mirrors are inclined at angle θ as shown in figure. Light rays are incident parallel to one of mirrors. Light will start retracing its path after the reflection if
View SolutionFor the given process :-
_E01_426_Q01.png)
Column-IColumn-II(A)Process J→K(P)W>0(B)Process K→L(q)W<0(C)Process L→M(r)Q>0(D)Process M→J(s)Q<0
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
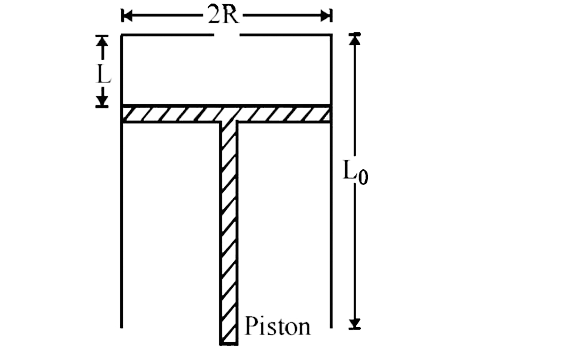
The piston is now pulled out slowly and held at a distance 2L from the top. The pressure in the cylinder between its top and the piston will then be
View SolutionA fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.

While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top is
View SolutionA fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
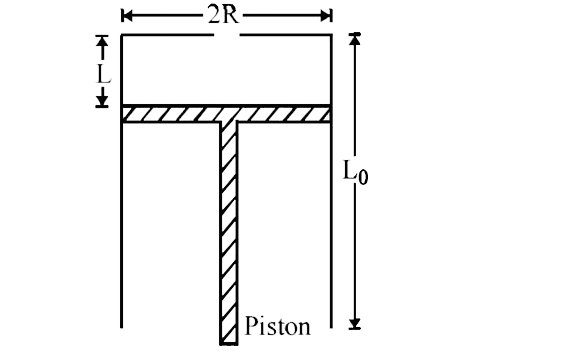
The piston is taken completely out of the cylinder. The hole at the top is sealed. A water tank is brought below the cylinder and put in a position so that the water surface in the tank is at the same level as the top of the cylinder as shown in the figure. The density of the water is ρ. In equilibrium, the height H of the water coulmn in the cylinder satisfies

View SolutionA cylinder vessel containing a liquid of density rho is closed by a smooth piston of mass m as shown. If atmospheric pressure is P_0 , radius of cylinder is r and height of liquid is h . Find (a) Pressure of liquid just below the piston (b) force at bottom of cylinder. .
View SolutionThere is a small hole in the bottom of a fixed container containing a liquid upto height 'h'. The top of the liquid as well as the hole at the bottom are exposed to atmosphere. As the liquid come out of the hole. (Area of the hole is 'a' and that of the top surface is 'A') :
View SolutionThe piston I s now pulled out slowly and held at a diatance 2L from the top. The pressure in the cylinder between its top and the piston will then be
View SolutionWhile the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a poistion where it can stay in equilibrium. In this condition, distance of the piston from the top is
View SolutionA fixed thermally conducting cylinder has radius R and length L_0 . The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P_0 . While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top is
View Solutionऊष्मा के चालक पदार्थ से बने तथा स्थिर रखे गए बेलन की त्रिज्या R तथा ऊँचाई L0 है | बेलन नीचे से खुला है तथा इसके ऊपरी सिरे में एक छोटा छेद है, जैसा कि चित्र में दिखाया गया है | एक पिस्टन जिसका द्रव्यमान M है, ऊपरी सतह से L दुरी पर पकड़ा हुआ है | वायुमण्डलीय दाब P0 है |
अब पिस्टन को बाहर की ओर धीरे - धीरे खिंचा जाता है तथा ऊपर से 2L दूरी पर पकड़ कर रखा जाता है, तब बेलन में ऊपरी सिरे तथा पिस्टन के बीच के भाग में दाब होगा |

View Solutionऊष्मा के चालक पदार्थ से बने तथा स्थिर रखे गए बेलन की त्रिजयका R तथा ऊँचाई I0 है | बेलन नीचे से खुला है तथा इसके ऊपरी सिरे में एक छोटा छेद है, जैसा कि चित्र में दिखाया गया है | एक पिस्टन जिसका द्रव्यमान M है, ऊपरी सतह से L दुरी पर पकड़ा हुआ है | वायुमण्डलीय दाब P0 है |

जब पिस्टन ऊपरी सिरे से 2L दूरी पर है, ऊपर के सिरे में स्थित छेद को बन्द कर दिया जाता है | पिस्टन को ऐसी जगह लाकर छोड़ा जाता है जहाँ वः संतुलन में रह सकता है | इस स्थिति में ऊपरी सिरे से पिस्टन की दूरी है |
View Solutionपिस्टन की ऊपर के पुष्ठ की दूरी 2L पर छिद्र को बन्द कर दिया जाता हैं फिर पिस्टन को छोड दिया जाता हैं जहाँ से पिस्टन सन्तुलन का स्थिति में रूक सकता हैं इस स्थिति में ऊपर के पृष्ठ से पिस्टन की दूरी होगी।
View Solution
