One mole of an ideal monatomic gas is taken round the cyclic process ABCA as shown in figure. Calculate
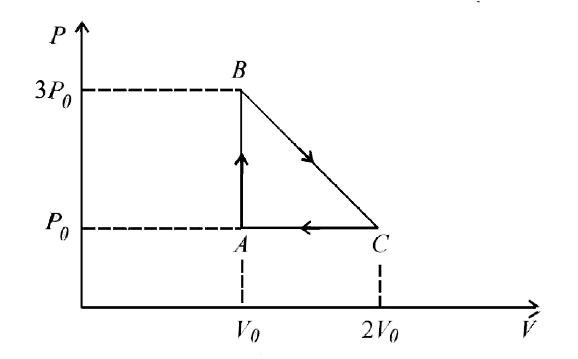
(a) the work done by the gas.
(b) the heat rejected by the gas in the path CA and the heat absorbed by the gas in the path AB,
(c) the net heat absorbed by the gas in the path BC,
(d) the maximum temperature attained by the gas during the cycle. Solution in Gujrati
The correct Answer is:(i) P0V0(ii)52P0V0,3P0V0(iii)12P0V0(iv)258P0V0R
(a)ABCA is a clockwise cyclic process.
_E01_438_S01.png)
∴ Work done by the gas
W = +Area pf triangle ABC
W=12 (base)(height) =12(2V0−V0)(3P0−P0)=P0V0
(b) No. of moles n=1 and gas is monoatomic , CV=32RandCP=52R⇒CVR=32andCPR=52
(i) Heat rejected in path CA
∴QCA=CPΔT=CP(Tf−Tl=CP((PfVfR−(PlVlR)=CPR(Pf−Vf−PlVl)
Substituting the values QCA=52(P0V0−2P0V0)=−52P0V0
Therefore,heat rejected in the process CAis52P0V0.
(ii) Heat absorbed in path AB: ∴QAB=CVΔT=CV(Tf−Ti)
=CV(PfVfR−PiViR)=CVR(PfVf−PiVi)
=32(PfVf−PiVi)=32(3P0V0−P0V0)=3P0V0
∴ Heat absorbed in the process ABis3P0V0
(c) Let QBC be the heat absorbed in the process BC Total heat absorbed
Q=QCA+QAB+QBC
Q=(−52P0V0)+(3P0V0)+QBC
Q=QBC+P0V02
Change in internal energy ΔU=0
Q=W ∴QBC+P0V02=P0V0
∴QBC=P0V02
∴ Heat absorbed in the process BC is P0V02
(d) Maximum temperature of the gas will some where between B and C . Line BC is a straight line . Therefore , P−V equation for the process BC can be written as
P=−mV+c,(y=mx+c)
Here , m=2P0V0andc=5P0∴P=−(2P0V0)V+5P0
Multiplying the equation by V
PV=−(2P0V0)V2+5P0V(PV=RTforn=1)
RT=−(2P0V0)V2+5P0V
⇒T=1R[5P0V−2P0V0V2]....(i)
For T to be maximum
dTdV=0⇒5P0−4P0V0,V=0⇒V=5V04
i.e., at V=5V04 (on line BC), temperature of the gas is maximum
From Equation (i) this maximum temperature will be Tmax=1R[5P0(5V04)−2P0V0(5V04)2]=258P0V0R
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B) (MCQ)9videos
GEOMETRICAL OPTICS
- BOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B) (MATCH THE COLUMN)3videos
GEOMETRICAL OPTICS
- BOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (A)73videos
GEOMETRICAL OPTICS
- BOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
Let ¯v,vrms and vp respectively denote the mean speed, the root-mean - square speed, and the most probable speed of the molecules in an ideal monoatomic gas at absolute temperature T. The mass of a molecule is m:-
12:22View SolutionFor the given process :-
_E01_426_Q01.png)
Column-IColumn-II(A)Process J→K(P)W>0(B)Process K→L(q)W<0(C)Process L→M(r)Q>0(D)Process M→J(s)Q<005:51View SolutionAn aluminium sphere of 20cm diameter is heated from 0∘C to 100∘C. Its volume changes by (given that the coefficient of linear expanison for aluminium (αAl=23×10−6/0C)
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
01:38View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.05:12View SolutionOne mole of an ideal monatomic gas is taken round the cyclic process ABCA as shown in figure. Calculate (a) the work done by the gas. (b) the heat rejected by the gas in the path CA and the heat absorbed by the gas in the path AB, (c) the net heat absorbed by the gas in the path BC, (d) the maximum temperature attained by the gas during the cycle.
17:11View SolutionAn ideal gas is taken round a cyclci thermodynamic process ABCA as shown if Fig. If the internal energy of the gas at point A is assumed zero while at B it is 50 J. The heat absorbed by the gas in the process BC is 90 J. (a) What is the internal energy og the gas at point C ? (b) How much heat energy is absorbed by the gas in the process AB? (c ) Find the heat energy rejected or absorbed by the gas in the process CA. (d) What is the net work done by the gas in the complete cycle ABCA ?
05:41View SolutionOne mole of ideal monatomic gas in taken in cyclice process ABCA as shown in the figure

Calculate :
(a) The work done by the gas
(b) The heat rejected by the gas in the path CA
(c) The net heat absorbed be the by gas in the path BC
(d) Maximum temperature obtained by the gas during the cycle.05:41View SolutionOne mole of ideal monoatmic gas is carried throught the reversible cyclic process as shown in figure. Calculate net heat absorbed by the gas in the path BC
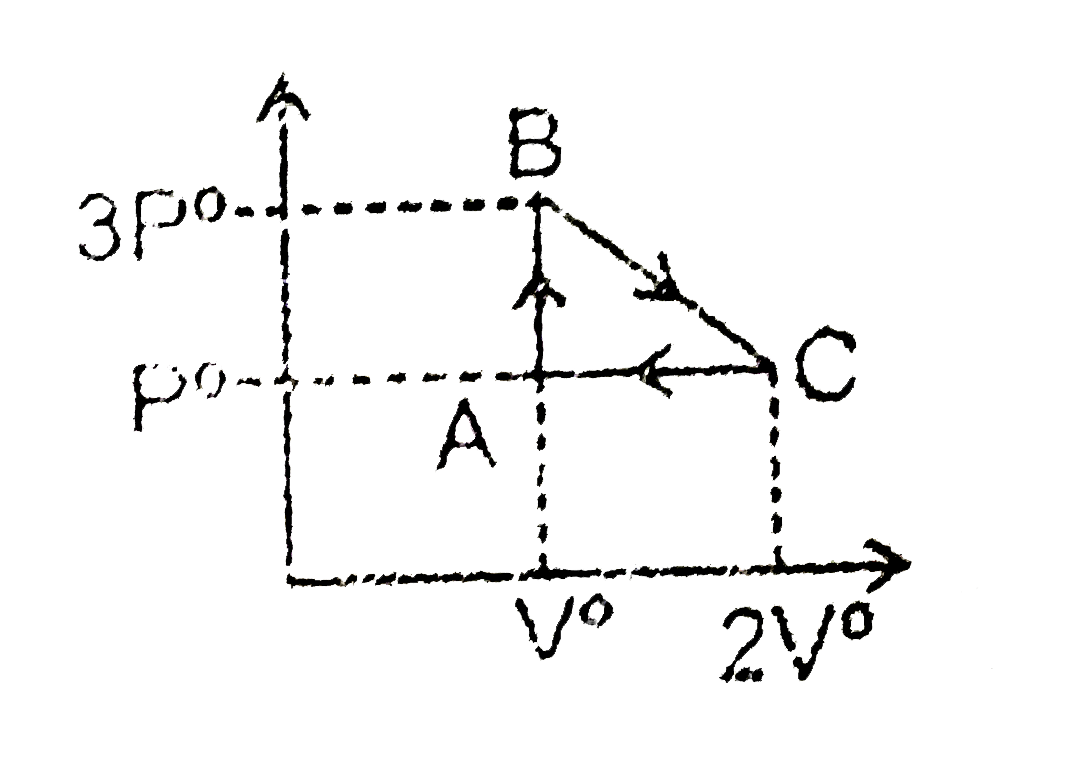 06:16View Solution
06:16View SolutionOne mole of ideal monoatomic gas is taken round the cyclic process as shown in figure. The heat rejected by the gas in the path is ………...and the heat absorbed by the gas in the path AB is ………...........
View Solutionएकपरमाणुक आदर्श गैस के 1 मोल को चित्र में दिखाए गए चक्रीय प्रक्रम ABCA में ले जाया जाता है | गणना कीजिए
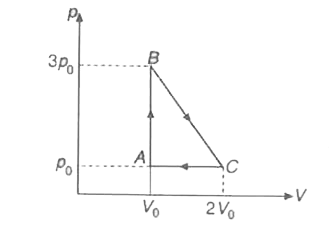
(a) गैस द्वारा किया गया कार्य |
(b) पथ CA में गैस द्वारा बहिष्कृत ऊष्मा तथा पथ AB में गैस द्वारा अवशोषित ऊष्मा |
(c ) पथ BC में गैस द्वारा अवशोषित नेट ऊष्मा |
(d) चक्र के दौरान गैस द्वारा अर्जित उच्चतम ताप |View Solutionएक आदर्श गैस को, चित्र में दर्शाये गये अनुसार चक्रीय प्रक्रम abca से गुजारा जाता है। ca पथ के अनुदिश गैस की आन्तरिक ऊर्जा में परिवर्तन -180 J है। ab पथ के अनुदिश, गैस 250 J ऊष्मा अवशोषित करती है तथा bc पथ के अनुदिश, गैस 60 J ऊष्मा अवशोषित करती है तो. पथ abc के अनुदिश, गैस द्वारा किया गया कार्य है
 10:51View Solution
10:51View Solutionएक आदर्श गैस को, चित्र में दर्शाये गये अनुसार चक्रीय प्रक्रम abca से गुजारा जाता है। ca पथ के अनुदिश गैस की आन्तरिक ऊर्जा में परिवर्तन -180 J है। ab पथ के अनुदिश, गैस 250 J ऊष्मा अवशोषित करती है तथा bc पथ के अनुदिश, गैस 60 J ऊष्मा अवशोषित करती है तो. पथ abc के अनुदिश, गैस द्वारा किया गया कार्य है
 01:54View Solution
01:54View SolutionA sample of an ideal gas is taken through the cyclic process abca and shown in the figure. The change in the internal energy of the gas along the path ca is -180J . The gas absorbs 250J of heat along the path ab and 60 J along the path bc. the work done by the gas along the path abc is:
05:42View SolutionOne mole of an ideal monoatomic gas is taken round the cyclic process ABCA as shown in figure. Calculate
The heat rejected by the gas in the path CA and heat absorbed in the path AB10:14View SolutionOne mole of an ideal monoatomic gas is taken round the cyclic process ABCA as shown in figure. Calculate
The net heat absorbed by the gas in the path BC.View Solution

