One end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:K4eAσLT3S+K
Rate of heat conduction through rod rate of the heat lost from right end of the rod.
∴KA(T1−T2)L=eAσ(T42−T4s) ……. (i)
Given that T2=Ts+ΔT
∴T42=(Ts+ΔT)4=T4s(1+ΔTTs)4
Using binomial expansion, we have
T42=T4s(1+4ΔTTs)(asΔT<<Ts)
∴T42−T4s=4(ΔT)(T3s)
Substituting in Eq.(i) , we have
K(T1−Ts−ΔT)L=4eσT3sΔT
⇒KT1−TsL=(4eσT3s+KL)ΔT
∴ΔT=KT1−Ts(4eσLT3s+K)
Comparing with the given relation, proportional constant = K4eσLT3s+K
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B) (MCQ)
9 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B) (MATCH THE COLUMN)
3 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (A)
73 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Let ¯v,vrms and vp respectively denote the mean speed, the root-mean - square speed, and the most probable speed of the molecules in an ideal monoatomic gas at absolute temperature T. The mass of a molecule is m:-
View SolutionFor the given process :-
_E01_426_Q01.png)
Column-IColumn-II(A)Process J→K(P)W>0(B)Process K→L(q)W<0(C)Process L→M(r)Q>0(D)Process M→J(s)Q<0
View SolutionAn aluminium sphere of 20cm diameter is heated from 0∘C to 100∘C. Its volume changes by (given that the coefficient of linear expanison for aluminium (αAl=23×10−6/0C)
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionFour identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmospere, find the temperature at B.

View SolutionA cylinder rod of length 1, thermal conductivity K and area of cross section A has one end in the furnace at temperature T_1 and the other end in surrounding at temperature T_2 . Surface of the rod exposed to the surrounding has emissivity e. Also T_2=T_s+DeltaT and T_sgt gt DeltaT . If T_1-T_s prop DeltaT ,find the proportionality constant.
View SolutionThe two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
View SolutionA rod of length L with sides fully insulated is made of a material whose thermal conductivity K varies with temperature as K=αT where α is constant. The ends of rod are at temperature T1 and T2(T2>T1) Find the rate of heat flow per unit area of rod .
View SolutionA cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T0 and the furnace is maintained at T1=T0+ΔT1. The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T2=T0+ΔT2[ΔT2<<T0]. The exposed surface of the rod has emissivity e. Prove that ΔT1 is proportional to ΔT2 and find the proportionality constant.
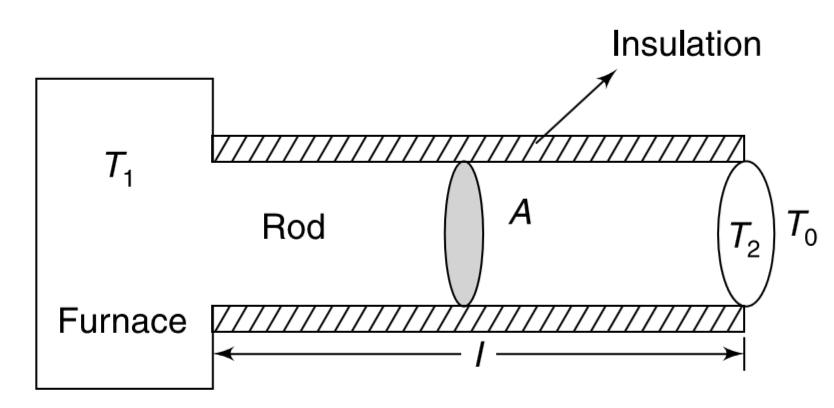
View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = alpha T, where alpha is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T_(1) and T_(2) (T_(1)gtT_(2)) . Heat current flowing through the rod will be
View SolutionCurved surface of a uniform rod is isolated from surrounding. Ends of the rod are maintained at temperatures T1 and T2(T1>T2) for a long time. At an instant, temperature T1 starts to decrease at a constant and slow rate. If thermal capacity of material of the rod is considered, then which of thefollowing statements is/are correct ?
View Solutionलम्बाई L तथा अनुप्रस्थ - क्षेत्रफल A वाली छड़ का एक सिरा T1 तापमान वाली भट्टी में रखा है | छड़ का दूसरा सिरा ताप T2 पर है | छड़ के पदार्थ की ऊष्मा चालकता K तथा उत्सर्जकताe है | दिया है : T2=Ts+ΔT, जहाँ ΔT<<Ts,Ts वातावरण का तापमान है | यदि ΔT∝(T1−Ts), तो अनुक्रमानुपाती नियतांक का मान ज्ञात कीजिए | मान कीजिए कि ऊष्मा का क्षय, केवल T2 ताप वाले सिरे से विकिरण के रूप में हो रहा है |

View SolutionThe two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperatures f_(1) and T_(2) rod in a steady state is given by :
View SolutionLet the length L and the two ends of a rod of constant intersection area A be two temperatures. T_(1) And T_(2) (whereas T_(1) gt T_(2) Is) being kept constant at. The rate of heat transfer from the rods to the stationary state, (dQ)/(dt) Will be
View SolutionConstant temperature of ends are T1 and T2 (where T1>T2) for a conducting rod of 'L' length and cross-sectional area A. What would be the rate of heat transfer in thermal steady state ?
View Solution
