In the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.
 Solution in Gujrati
Solution in Gujrati
If m is equilibrium tension in string must be mg and spring is stretched by h so that mg=kh. If the displace the block downward by a distance A and relesed, it starts executing SHM with amplitude A. During its ocillation we consdier the block at a displacement x below the equilibrium position, if it is moving at a speed b at this position, the pulley will be rotating at an angular speed ω given as ω=vr
_S01_025_S01.png)
Thus at this position the total energy of oscillating system is ET=12mv2+12Iω2+12k(x+h)2−mgx
Differentiating with respect to time,
we get dETdt=12m(2vdvdt)+12I(1r2)(2vdvdt)+12k[2(x+h)dxdt]−mg(dxdt)=0
or mva+Ir2va+k(x+h)v−mgv=0 or a+⎛⎜⎝km+Ir2⎞⎟⎠x=0 [as mg=kg]
comparing above equation with standard differentional equation of SHM we get ω=
⎷⎛⎜⎝km+Ir2⎞⎟⎠
Thus time period of oscillation is T=2πω=2π
⎷m+Ir2k
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES29videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01117videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A simple pendulum has time period 2s. The point of suspension is now moved upward accoding to relation y=(6t−3.75t2)m where t is in second and y is the vertical displacement in upward direction. The new time period of simple pendulum will be
02:37View SolutionThe equation of motion of a particle of mass 1g is d2xdt2+π2x=0, where x is displacement (in m) from mean position. The frequency of oscillation is (in Hz)
09:07View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
08:58View SolutionChoose the correct statement:
07:12View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
02:34View SolutionFigure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m . If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).
06:28View SolutionIn the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.
02:32View SolutionIn the device shown in Fig, the block m is displaced down slightly and released. It starts oscillating. Pulleys are smooth and massless string and springs are also massless. Find time period of oscillations.
 06:03View Solution
06:03View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
 05:00View Solution
05:00View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and ablock of mass m. If the block is slightly displaced vertically down from its equillibrium position and then released, find the period of its vertical oscillation in cases (a) & (b).
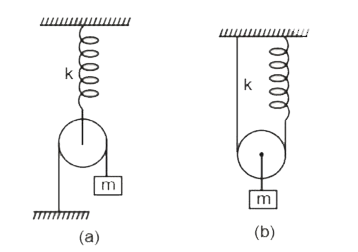 04:01View Solution
04:01View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is
 07:04View Solution
07:04View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
 04:37View Solution
04:37View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
04:07View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
 01:30View Solution
01:30View SolutionFigure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).
 07:32View Solution
07:32View Solution

