An oscillation is superposition of three harmonic oscillations and decribed by the equation x=Asin2πυ1 where A changes with time according to A=A0(1+cos2πυ2t) with A0 to be constant. The frequencies of pure harmonic oscillations forming this oscillation are Solution in Gujrati
(a)υ1,υ2,υ1−υ2
(b)υ1,υ2,υ1+υ2
(c)υ1,υ1+υ2,υ1−υ2
(d)υ2,υ1+υ2,υ1−υ2
The correct Answer is:B
x=A0(1+cos2πγ2t)sin(πγ1)
=A0[sin2πγ1t+cos2πγ2t+sin2πγ1t]
=A0[sin2πγ1t+12sin(2π(γ1+γ2)t−12sin(2π(γ1−γ2t)]
Required ratio =v1:(v1−v2):(v1+v2)
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-0219videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column1videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES29videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A mass M is performing linear simple harmonic motion. Then correct graph for acceleration a and corresponding linear velocity v is
01:51View SolutionColumn-I gives different situtions in which bodes are floating in liquid. Column-II gives correspoding time periods of oscillation.
_E01_069_Q01.png)
A cube floating in liquid.05:22View SolutionA simple pendulum has time period 2s. The point of suspension is now moved upward accoding to relation y=(6t−3.75t2)m where t is in second and y is the vertical displacement in upward direction. The new time period of simple pendulum will be
02:36View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
02:23View SolutionChoose the correct statement:
01:59View SolutionAn oscillation is superposition of three harmonic oscillations and decribed by the equation x=A sin 2pi upsilon_(1) where A changes with time according to A=A_(0)(1+cos 2pi upsilon_(2)t) with A_0 to be constant. The frequencies of pure harmonic oscillations forming this oscillation are
03:35View SolutionThe superposition of two harmonic oscillations of the same direction results in the oscillation of a point according to the law x=a cos 2.1 t cos 50.0 t , where t is expressed in seconds. Find the angular frequencies of the constituent oscillations and the period with which they beat.
05:08View SolutionA mass m oscillates with simple harmonic motion with frequency f=ω2πand amlitude A on a spring with constant K. therefore
View SolutionThe velocity-time diagram of a harmonic oscillator is shown in the adjoining figure. The frequency of oscillation is
03:36View SolutionIn forced oscillations , a particle oscillates simple harmonically with a frequency equal to
01:35View Solution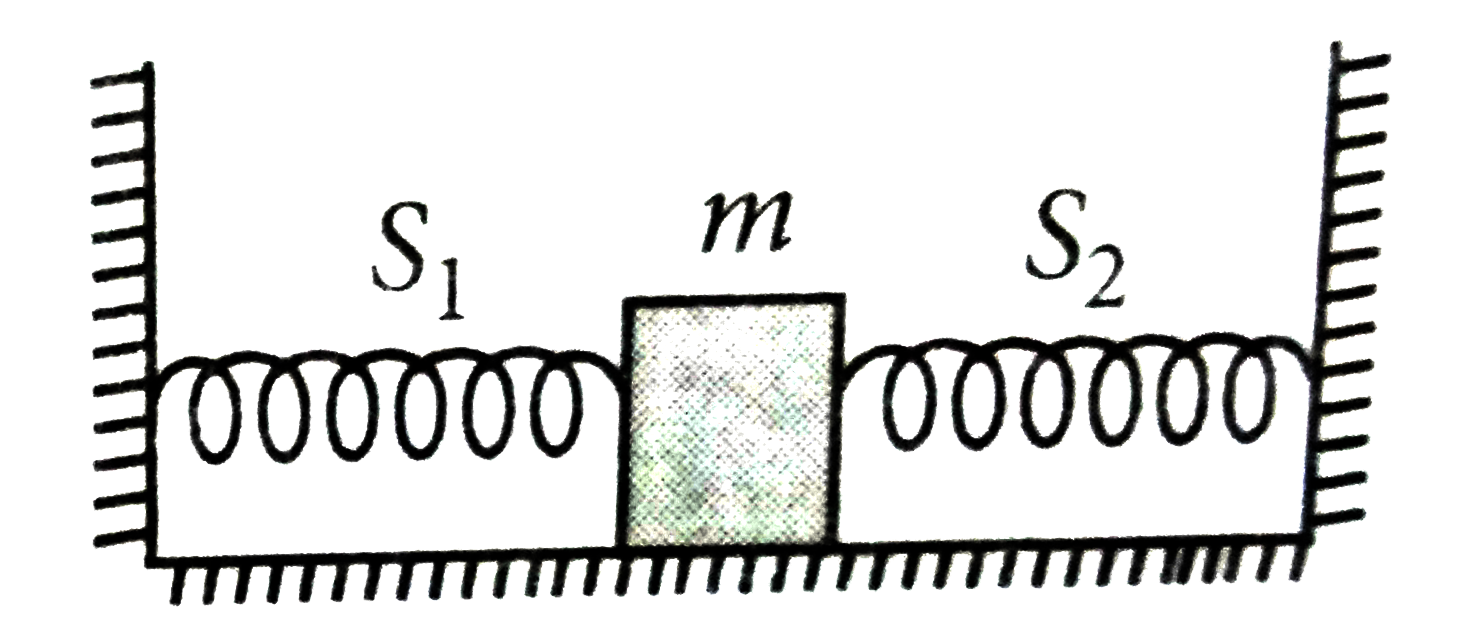
When a mass m is connected individually to two springs S1andS2, the oscillation frequencies are υ1andυ2. If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be01:58View SolutionWhat is meant by angular harmonic oscillations? Compute the time period of angular harmonic oscillation. Time period and frequency of angular SHM:
01:19View SolutionFor a simple harmonic oscillator the frequency of oscillation is independent of
00:15View SolutionWhen a mass m is connected individually to two springs S_(1) and S_2 , the oscillation frequencies are upsilon_(1) and upsilon_(2) . If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be
01:29View SolutionFor a simple harmonic oscillator the frequency of oscillation is independent of
35:21View Solutionकिसी स्प्रिंग से लटके हुए m द्रव्यमान के दोलनों की आवृत्ति υ1 है। यदि स्प्रिंग की लम्बाई को आधा कर दिया जाए, तो समान द्रव्यमान υ2 आवृत्ति के साथ दोलन करता है। υ2/υ1 का मान होगा
59:12View Solution

