For all positive numbers x,y,z the product equals Solution in Gujrati
The correct Answer is:A
Step by step video & image solution for For all positive numbers x,y,z the product ((1)/(x+y+z))((1)/(x)+(1)/(y)+(1)/(z))((1)/(xy+yz+zx))((1)/(xy)+(1)/(yz)+(1)/(zx)) equals by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - RACE 4
10 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - RACE 5
10 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - RACE 2
9 Videos
- LOGARITHMSBOOK - ALLEN CHAPTER - LOGARITHMSEXERCISE - All Questions
103 Videos
- SEQUENCE AND PROGRESSIONBOOK - ALLEN CHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)
10 Videos
Similar Questions
In the figure, when the outer circles all have radii 'r', then the radius of the inner circle will be
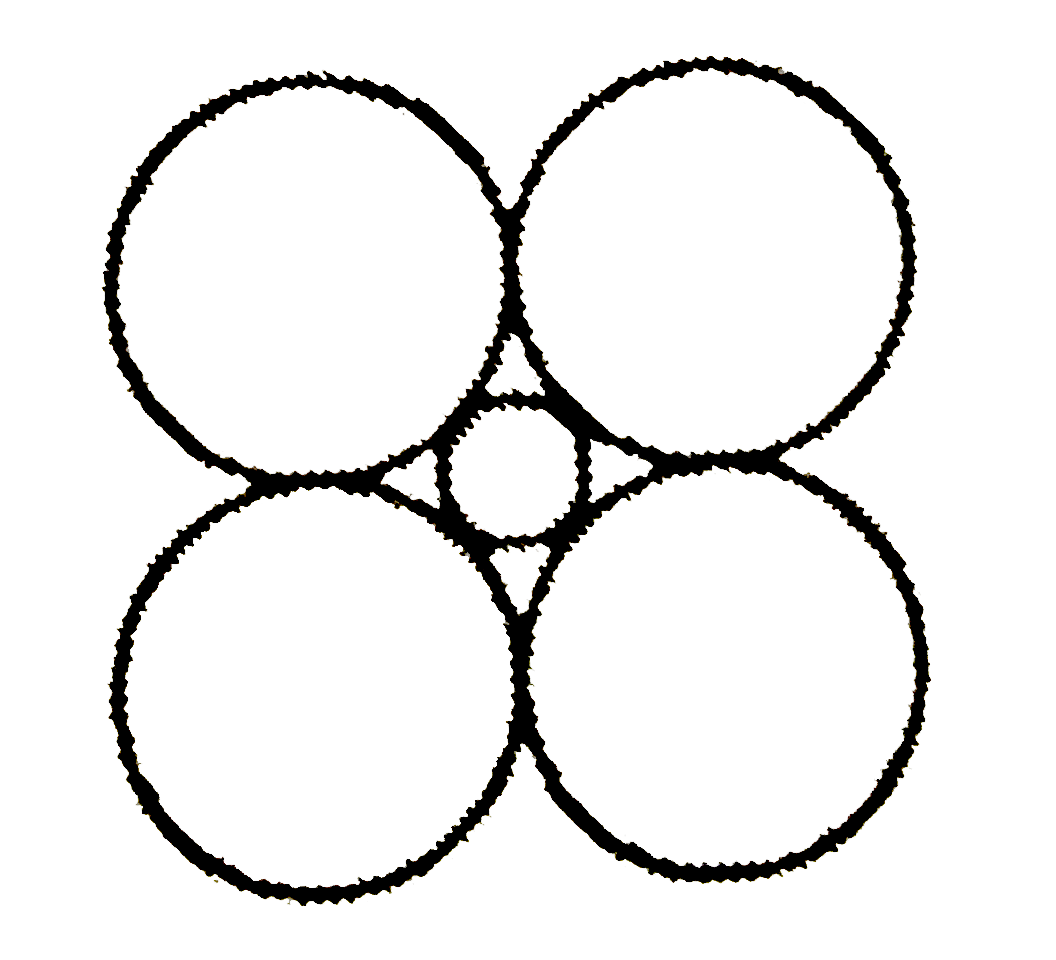
View SolutionIf BC passes through centre of the circle, then the area of the shaded region in the given figure is:
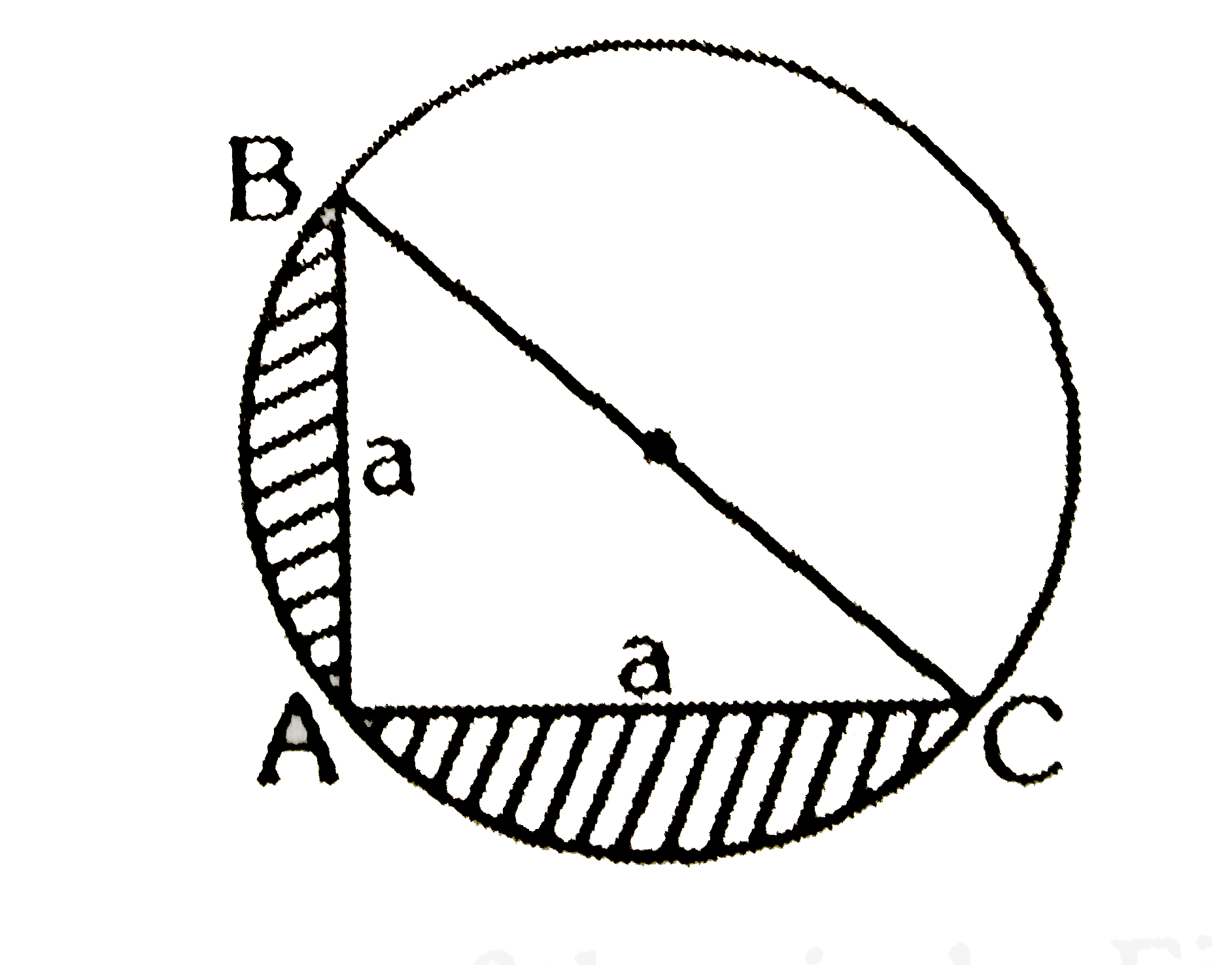
View SolutionIf x,y,z are all different real numbers, then 1(x−y)2+1(y−z)2+1(z−x)2=(1x−y+1y−z+1z−x)2
View SolutionThe value of N satisfying (log)a[1+(log)b {1+(log)c(1+(log)pN)}]=0 is-
a.4 b. 3 c.2 d. 1
View SolutionThe minimum value of the sum of real numbers a−5,a−4,3a−3,1,a8 and a10 with a>0 is
View Solutionxy+yz+zx=1rArr(x)/(1+x^(2))+(y)/(1+y^(2))+(z)/(1+z^(2))=
View SolutionFor all positive numbers x,y,z the product (1x+y+z)(1x+1y+1z)(1xy+yz+zx)(1xy+1yz+1zx) equals
View Solutionनिम्न को सिद्ध कीजिए ।
cot−1(xy+1x−y)+cot−1(yz+1y−z)+cot−1(zx+1z−x)=0(0<xy,yz,zx<1)
View Solutionसिद्ध कीजिए -
cot−1(xy+1x−y)+cot−1(yz+1y−z)+cot−1(zx+1z−x)=0,0<xy,yz,zx<1.
View SolutionIf x,y,z are in A. P. then 1yz,1zx,1xy are in-
View SolutionIf xy+yz+zx=1, then x1+x2+y1+y2+z1+z2=
View Solutionसिद्ध कीजिए- tan−1x−y1+xy+tan−1y−z1+yz+tan−1z−x1+zx=0,(0<xy,yz,zx<1)
View Solution∣∣ ∣ ∣∣1x1y1zx2y2z2yzzxxy∣∣ ∣ ∣∣
View Solutionसिद्ध कीजिये की -∣∣ ∣ ∣∣1yzy+z1zxz+x1xyx+y∣∣ ∣ ∣∣=(x−y)(y−z)(z−x)
View SolutionIf xy+yz+zx=1 find x+y1−xy+y+z1−yz+z+x1−zx= ?
View Solution
