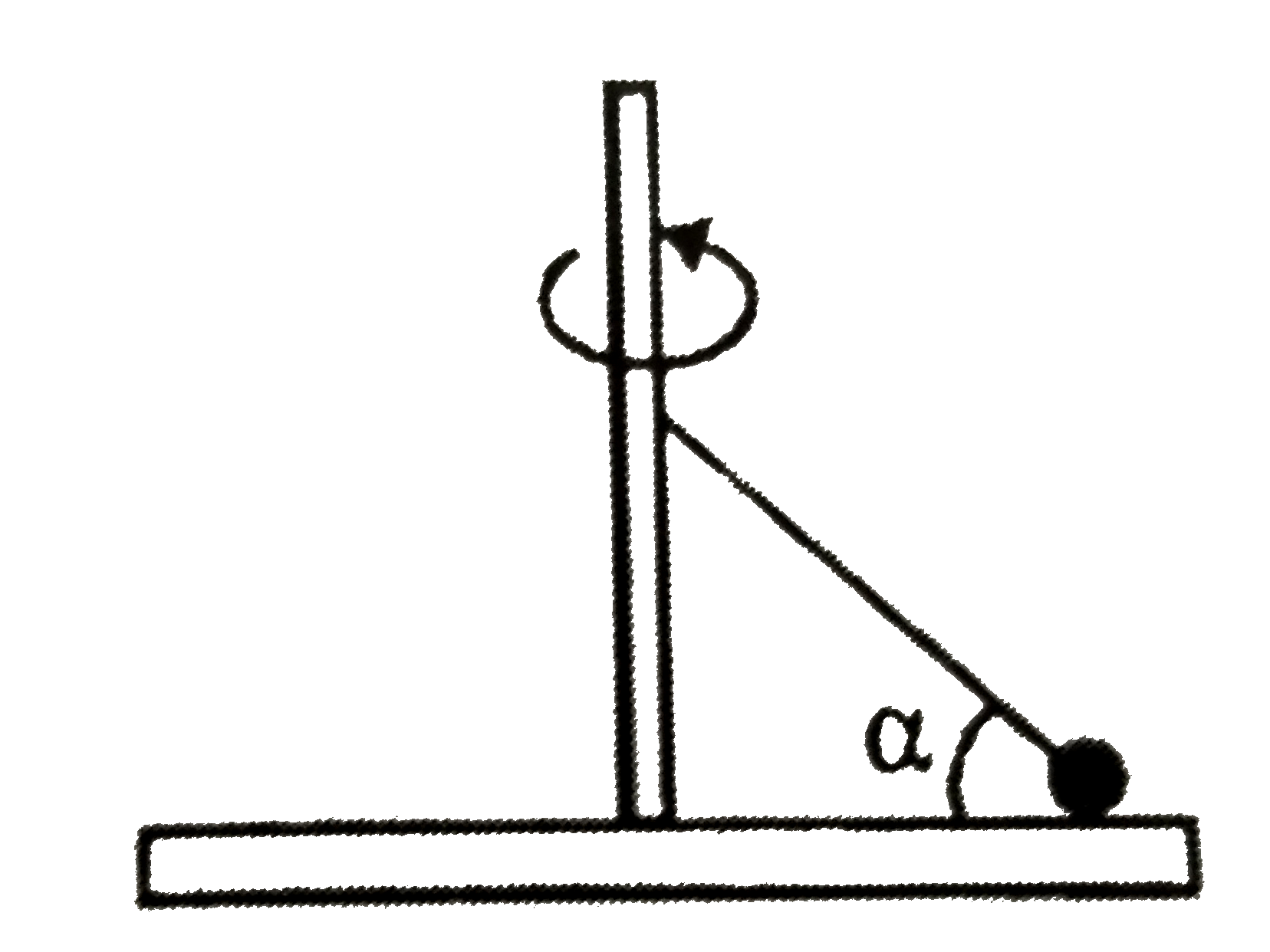
A circular platform rotates around a vertical axis with angular velocity . On the platform is a ball of mass 1kg, attached to the long axis of the platform by a thin of length of 10cm . Find normal force exerted by the ball on the platform (in newton). Friction is absent.
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:5
Step by step video & image solution for A circular platform rotates around a vertical axis with angular velocity omega=10rad//s. On the platform is a ball of mass 1kg, attached to the long axis of the platform by a thin of length of 10cm (alpha=30^(@)). Find normal force exerted by the ball on the platform (in newton). Friction is absent. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(S-2)
6 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(O-1)
22 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (S-1)
10 Videos
- BASIC MATHSBOOK - ALLEN CHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
Similar Questions
A stone is launched upward at 45∘ with speed v0. A bee follow the trajectory of the stone at a constant speed equal to the initial speed of the stone.
(a) Find the radius of curvature at the top point of the trajectory.
(b) What is the acceleration of the bee at the top point of the trajectory? For the stone, neglect the air resistance.
View SolutionThe area of the parallelogram represented by the vectors →A=2ˆi+3ˆj and →B=ˆi+4ˆj is
View SolutionA stone tied at the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 25 revolutions in 14 s, what is the magnitude of acceleration of the stone ?
View SolutionFind dydx for the following :
(i) y=x7/2 (ii) y=x−3
(iii)y=x (iv) y=x5+x3+4x1/2+7
(v) y=5x4+6x3/2+9x (vi) y=ax2+bx+C
(Vii)y=3x^(5)-3x-1/x
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionA child of mass m is standing, on the periphery of a circular platform of radius R , which can rotate about its central axis. The moment of inertia of the platform is I . Child jumps off from the platform with a velocity u tangentially relative to the platform. Find the angular speed of the platform after the child jumps off.
View SolutionSuppose in the previous poroblem, the child stays at rest on the platform and one of hils firend throws a ball of mas m_(1) towards thim with a velocity of v from a direction tangential to the platform and the child on the platform catches the ball. Find the angular velocity of the platform after he catches the ball.
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity omega_(0) . When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),
View SolutionA woman of mass m stands at the edge of ,a solid cylindrical platform of mass M and radius R. At t=0 the platform is rotating with negligible friction at angular velocity ω0 about a vertical axis passing through the centre. The woman begins to walk with speed v, relative to the platform, towards the centre of the platform:
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform Now, the platform is given an angular velocity omega_(0) . When the tortoise moves along a chord of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform will vary with time t as -
View SolutionA coin is placed on a rotating platform at distance 'r' from its axis of rotation . To avoid the skidding of coin from rotating platform , the maximum angular velocity omega is
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now, the platform is given an angular velocity ω0 . When the tortoise moves along a chord of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform will vary with time t as
View Solutionएक वृत्ताकार प्लेटफॉर्म क्षैतिज तल में अपने केंद्र से जाने वाली ऊर्ध्वाधर अक्ष के परितः घूमती है। प्लेटफॉर्म के सिरे पर एक कछुआ बैठा है। प्लेटफॉर्म को ω0 कोणीय वेग से घुमाया जाता है । जब कछुआ प्लेटफार्म की जीवा के अनुदिश नियत वेग v (प्लेटमफॉर्म के सापेक्ष) से गति करता है तो प्लेटफॉर्म के कोणीय वेग ω(t) तथा t के साथ परिवर्तन प्रदर्शित होगा
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity ω0. When the tortoise moves along a chord of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform ω(t) will vary with time t as :
View Solution80 किग्रा का व्यक्ति वृत्तीय प्लेटफॉर्म के रिम (घेरे) में खड़ा है प्लेटफॉर्म का द्रव्यमान 200 किग्रा है तथा यह अपनी अक्ष के परितः घूर्णन कर रहा है। व्यक्ति सहित प्लेटफॉर्म 12 चक्र/मिनट की दर से घूर्णन करता है। यदि व्यक्ति प्लेटफॉर्म के केन्द्र की ओर जाता है, तब घूर्णन चाल होगी
View SolutionA person is standing on a platform rotating with an angular speed w, with stretched hands carrying equal masses each of m. Now he releases the masses such that they fall on the platform. The new angular velocity of platform would be:
View Solution
