A particle is moving along a circular path ofradius R in such a way that at any instant magnitude of radial acceleration & tangential acceleration are equal. 1f at t = 0 velocity of particle is V0. Find the speed of the particle after time t=(R)/(2V0)Solution in Gujrati
The correct Answer is:2V0
Step by step video & image solution for A particle is moving along a circular path ofradius R in such a way that at any instant magnitude of radial acceleration & tangential acceleration are equal. 1f at t = 0 velocity of particle is V_(0). Find the speed of the particle after time t=(R )//(2V_(0)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(O-1)
22 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - MCQ
14 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - Dynamics of circular motion
8 Videos
- BASIC MATHSBOOK - ALLEN CHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
Similar Questions
The area of the parallelogram represented by the vectors →A=2ˆi+3ˆj and →B=ˆi+4ˆj is
View SolutionA car is moving with constant speed on a rough banked road.

Figure shows the free body diagram of car in three situation A, B & C respectively:
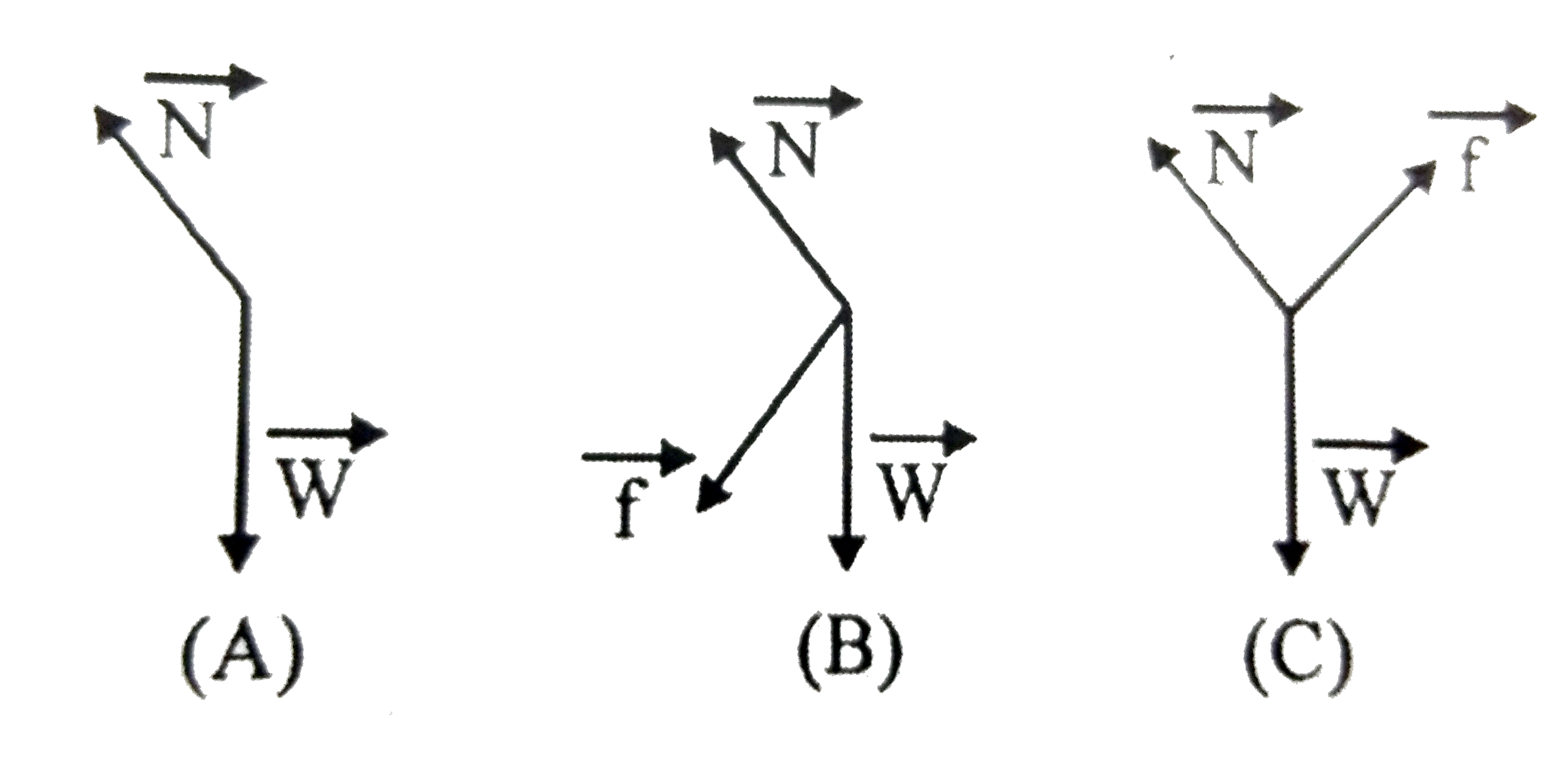
View SolutionThe ball of mas m moves with speed v againest a smooth , fixed vertical circular groove of radius R kept on smooth horizontal surface find the
a. normal reaction of the floor or the ball.
b. normal reaction of the vertical wall on the ball.
View SolutionFind dydx for the following :
(i) y=x7/2 (ii) y=x−3
(iii)y=x (iv) y=x5+x3+4x1/2+7
(v) y=5x4+6x3/2+9x (vi) y=ax2+bx+C
(Vii)y=3x^(5)-3x-1/x
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionA particle is moving with a constant angular acceleration of 4rad//s^(2) in a circular path. At time t=0 , particle was at rest. Find the time at which the magnitudes of centripetal acceleration and tangential acceleration are equal.
View SolutionA particle is moving along a circular path of radius of R such that radial acceleration of particle is proportional to t2 then
View SolutionA particle is moving on a circle of radius R such that at every instant the tangential and radial accelerations are equal in magnitude. If the velocity of the particle be v_(0) at t=0 , the time for the completion of the half of the first revolution will be
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View Solutiona particle is moving in a circle of radius R in such a way that at any instant the normal and the tangential component of its acceleration are equal. If its speed at t=0 is v0 then time it takes to complete the first revolution is Rαv0(1−e−βπ). Find the value of (α+β).
View SolutionA particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
View SolutionFor a particle moving along circular path, the radial acceleration ax is proportional to time t. If at is the tangential acceleration, then which of the following will be independent of time t.
View SolutionA particle is moving in a circle of radius R in such a way that at any instant the tangential retardation of the particle and the normal acceleration of the particle are equal. If its speed at t=0 is v0, the time taken to complete the first revolution is
View SolutionA particle is moving in a circle of radius R in such a way that at any instant the normal and tangential components of the acceleration are equal. If its speed at t=0 is u_(0) the time taken to complete the first revolution is :
View SolutionA particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal acceleration are equal in moduli. At the initial moment t=0 the speed of the particle equals V0 then
The total acceleration of the particle as function of velocity and distance covered
View SolutionThe tangential and radial acceleration of a particle are a(t) and a(r) respectively. The motion of a particle is circular if
View Solution
