|→a.→b|=√3|→a×→b|, then the angle between →aand→b is:Solution in Gujrati
π6
π4
π3
π2
The correct Answer is:A
Step by step video & image solution for "|"oversetrightarrow(a).oversetrightarrow(b)"|"=sqrt3"|"oversetrightarrow(a)xxoversetrightarrow(b)"|", then the angle between oversetrightarrow(a)andoversetrightarrow(b) is: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - MCQ
14 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - Martrix match
1 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(S-2)
6 Videos
- BASIC MATHSBOOK - ALLEN CHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
Similar Questions
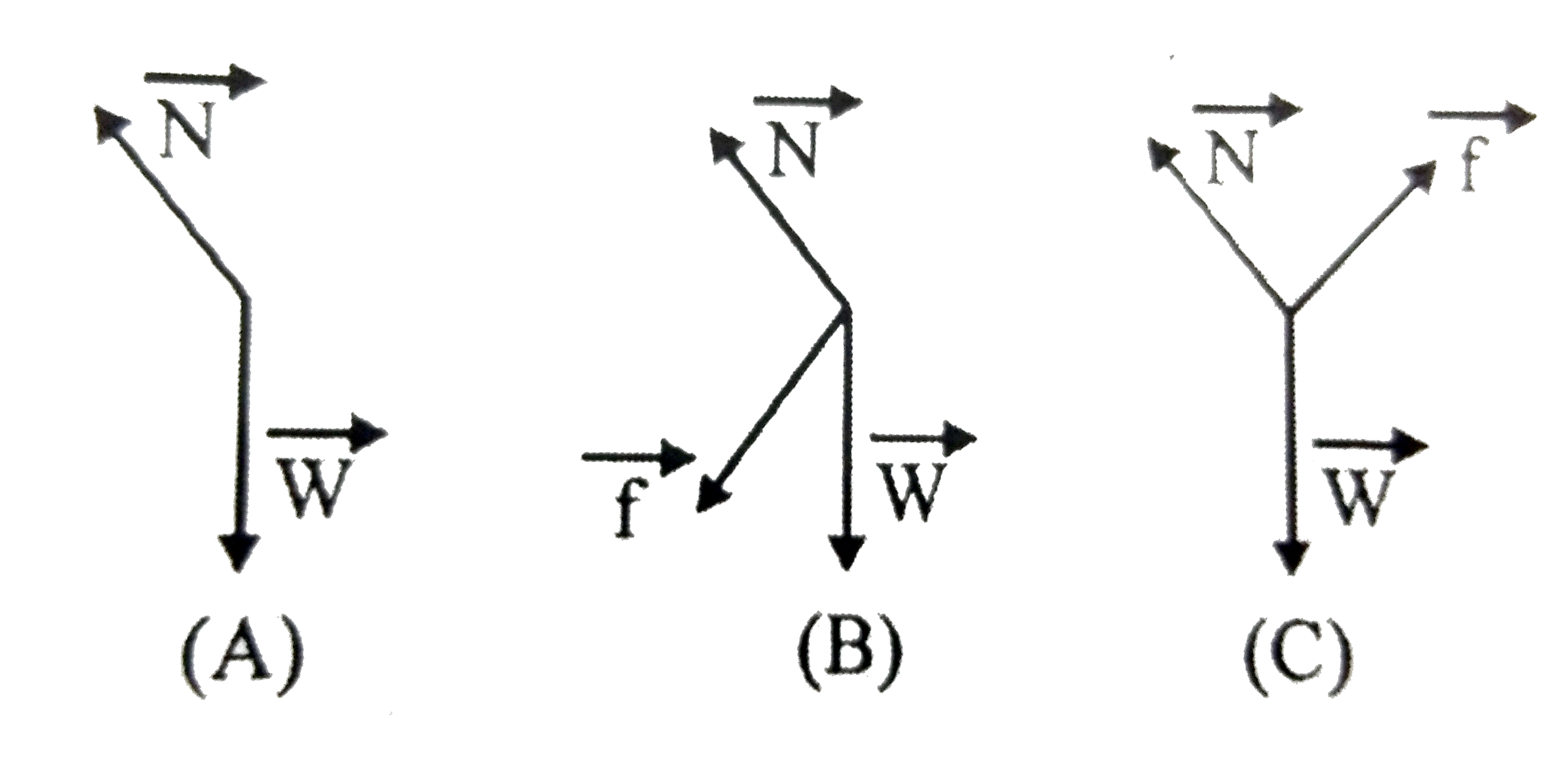
A car is moving with constant speed on a rough banked road.

Figure shows the free body diagram of car in three situation A, B & C respectively:
View SolutionA block is placed on a horizontal table which can rotate about its axis.The block is placed at certain distance from centre as shown in figure. Table rotates such that particle does not slide. See possible direction of net acceleration of block at the instant shown in figure
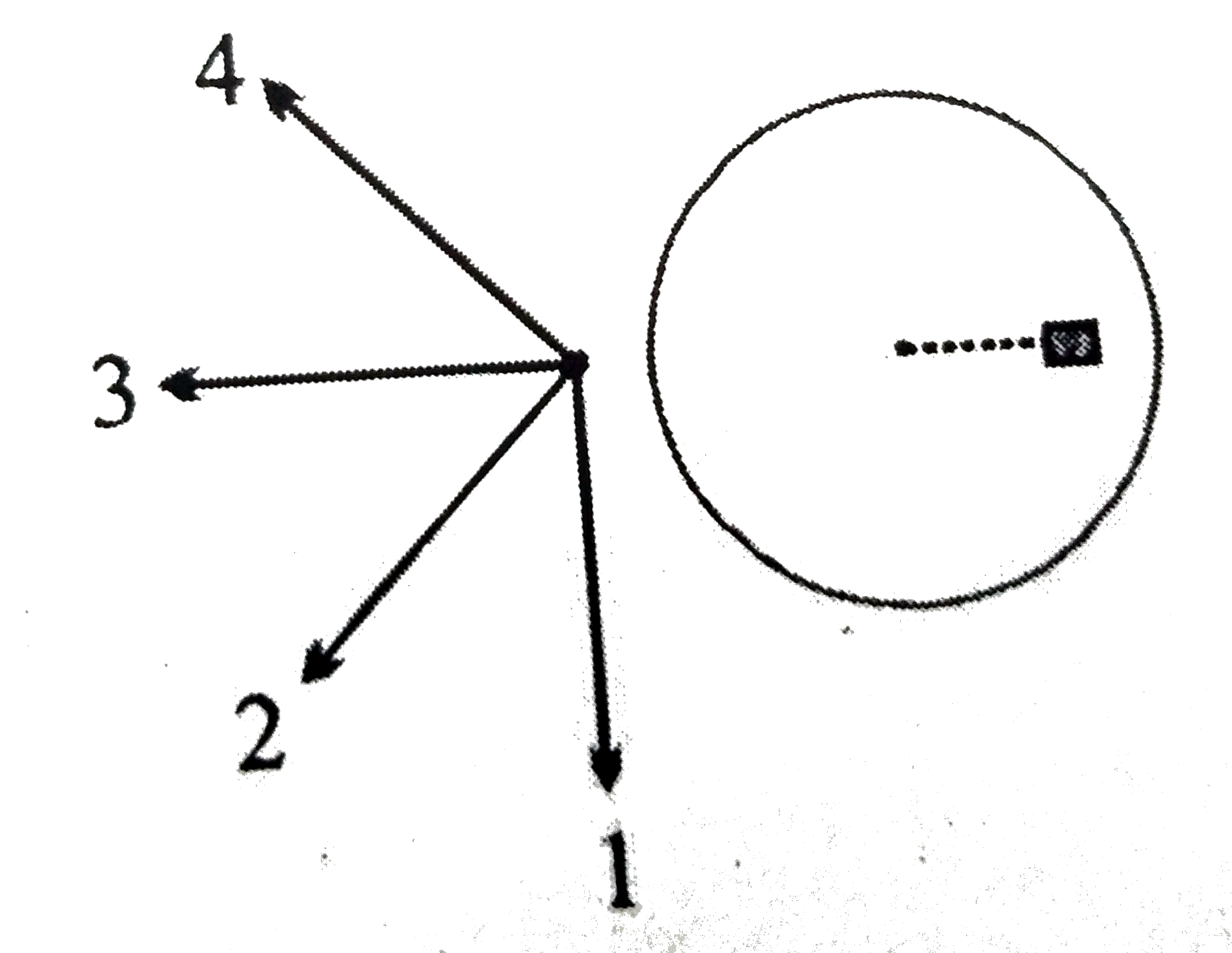
Column-IColumn-II(A)When rotation is clockwise with constant ω(P)1(B)When rotation is clock wise with decreasing ω(Q)2(C)When rotation is clockwise with increasing ω(R)3(D)Just after clockwise rotation beings from rest(S)4
View SolutionA stone is launched upward at 45∘ with speed v0. A bee follow the trajectory of the stone at a constant speed equal to the initial speed of the stone.
(a) Find the radius of curvature at the top point of the trajectory.
(b) What is the acceleration of the bee at the top point of the trajectory? For the stone, neglect the air resistance.
View SolutionFind dydx for the following :
(i) y=x7/2 (ii) y=x−3
(iii)y=x (iv) y=x5+x3+4x1/2+7
(v) y=5x4+6x3/2+9x (vi) y=ax2+bx+C
(Vii)y=3x^(5)-3x-1/x
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionChoose the correct options-
(1) Inertia ∝ mass
(2) 1 newton=105 dyne
(3) Thrust on rocket →F=ΔMΔt →V−M→g
(4) Apparent weight of a body in the accelerated lifts is W=m (g+a).
View SolutionChoose the correct statements-
(1) For equilibrium of a body under the action of concurrent forces →F1+→F2+→F3+.......→Fn=0
(2) If the downward acceleration of the lift is a = g, then the body will experience weightlessness.
(3) If the downward acceleration of the body is a gt g, then the body will rise up to the ceiling of lift
(4) If the downward acceleration of the lift is a gt g, then the body will experience weightlessness.
View SolutionA body is executing circular motion in the vertical plane containing directions. If the direction of velocity (oversetrightarrow(v)) at the top most point is towards west, what is the direction of angular velocity (oversetrightarrow(omega))?
View SolutionIf the magnitude of velocity in the previous question is decreasing with time, what is the direction of f angular acceleration (oversetrightarrow(alpha))?
View SolutionIf a + b + c = 0 and |a| = 1, |b| = 1, |c| =√3 ,then the angle between a and b is
View SolutionFind the acute angles A and B such that cot(A+B)=1√3andsec(A−B)=2√3.
View Solutionयदि →A+→B=C तथा A=√3,B=√3 तशा C=3, A तथा B के बीच कोण है
View SolutionA force →F=ˆi+5ˆj+7ˆk acts on a particle and displaces it through →s=6ˆi+9ˆk. Caldulate the work done if the force is in newton and displacement in metre.
View SolutionGive the expression for work done if angle between force →F and displacement →S is θ. Also find the dimensions and S.I. unit of work.
View SolutionWork done by a force is given by w=→F.→S where →F is the force and →S is the displacement. Show that : Work done is also equal to change in K.E.
View SolutionWork done by a force is given by w=→F.→S where →F is the force and →S is the displacement. Show that : Work done is also equal to change in potential energy using this expression.
View Solution
