A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
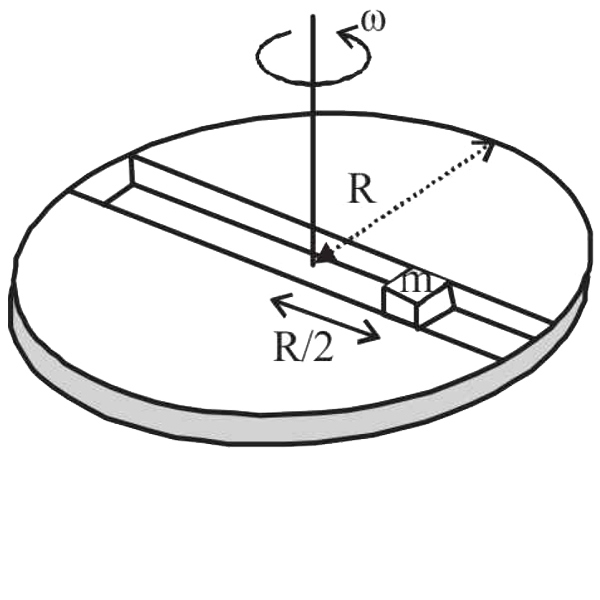
The distance r of the block at time is Solution in Gujrati
−mω2Rcosωtˆj−mgˆk
mω2Rsinωtˆj−mgˆk
12mω2R(eωt−e−ωt)ˆj+mgˆk
12mω2R(e2ωt−e2−ωt)ˆj+mgˆk
The correct Answer is:C
Step by step video & image solution for A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity omega is an example of non=inertial frame of reference. The relationship between the force vecF_(rot) experienced by a particle of mass m moving on the rotating disc and the force vecF_(in) experienced by the particle in an inertial frame of reference is vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega. where vecv_(rot) is the velocity of the particle in the rotating frame of reference and vecr is the position vector of the particle with respect to the centre of the disc. Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed omega about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (vecomega=omegahatk). A small block of mass m is gently placed in the slot at vecr(R//2)hati at t=0 and is constrained to move only along the slot. The distance r of the block at time is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
For a particle in uniform circular motion , the acceleration →a at a point p(R,θ) on the circle of radiu R is ( Here θ is measured from the x−aξs )
02:30View SolutionFind dydx for the following :
(i) y=x7/2 (ii) y=x−3
(iii)y=x (iv) y=x5+x3+4x1/2+7
(v) y=5x4+6x3/2+9x (vi) y=ax2+bx+C
(Vii)y=3x^(5)-3x-1/x20:36View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
20:36View SolutionNON-INERTIAL FRAME OF REFERENCE
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity omega is an example of non=inertial frame of reference. The relationship between the force vecF_(rot) experienced by a particle of mass m moving on the rotating disc and the force vecF_(in) experienced by the particle in an inertial frame of reference is vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega . where vecv_(rot) is the velocity of the particle in the rotating frame of reference and vecr is the position vector of the particle with respect to the centre of the disc. Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed omega about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (vecomega=omegahatk) . A small block of mass m is gently placed in the slot at vecr(R//2)hati at t=0 and is constrained to move only along the slot. The distance r of the block at time is
04:45View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity omega is an example of non=inertial frame of reference. The relationship between the force vecF_(rot) experienced by a particle of mass m moving on the rotating disc and the force vecF_(in) experienced by the particle in an inertial frame of reference is vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega . where vecv_(rot) is the velocity of the particle in the rotating frame of reference and vecr is the position vector of the particle with respect to the centre of the disc. Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed omega about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (vecomega=omegahatk) . A small block of mass m is gently placed in the slot at vecr(R//2)hati at t=0 and is constrained to move only along the slot. The net reaction of the disc on the block is
05:11View SolutionAssertion : A reference frame attached to earth is an inertial frame of reference.
Reason : The reference frame which has zero acceleration is called a non inertial frame of reference.03:25View SolutionIn an inertial frame of reference, the magnetic force on a moving charged particle is F. Its value in another inertial frame of reference will be
04:09View SolutionDistinguish between inertial and non-inertial frames of reference.
02:46View SolutionDefine inertial and non-inertial frames of reference with example.
01:31View SolutionDefine inertial frame and non-inertial frame. Is earth an inertial frame of reference?
07:39View Solution(A) : A reference frame attached to earth is a non inertial frame of reference.
(R) : The reference frame which has an acceleration is called a non inertial frame of reference.04:30View SolutionIn an inertial frame of reference, the magnetic force on a moving charged particle is F. Its value in another inertial frame of reference will be
04:53View SolutionExplain inertial frame of reference and non- inertial frame of reference.
07:36View SolutionDistinguish between :Inertial frame of reference & Non - Inertial frame of reference.
07:02View SolutionWhat is frame of reference? Explained the terms: (i) inertial frame of reference (ii) non-inertial frame of reference
03:27View Solution

