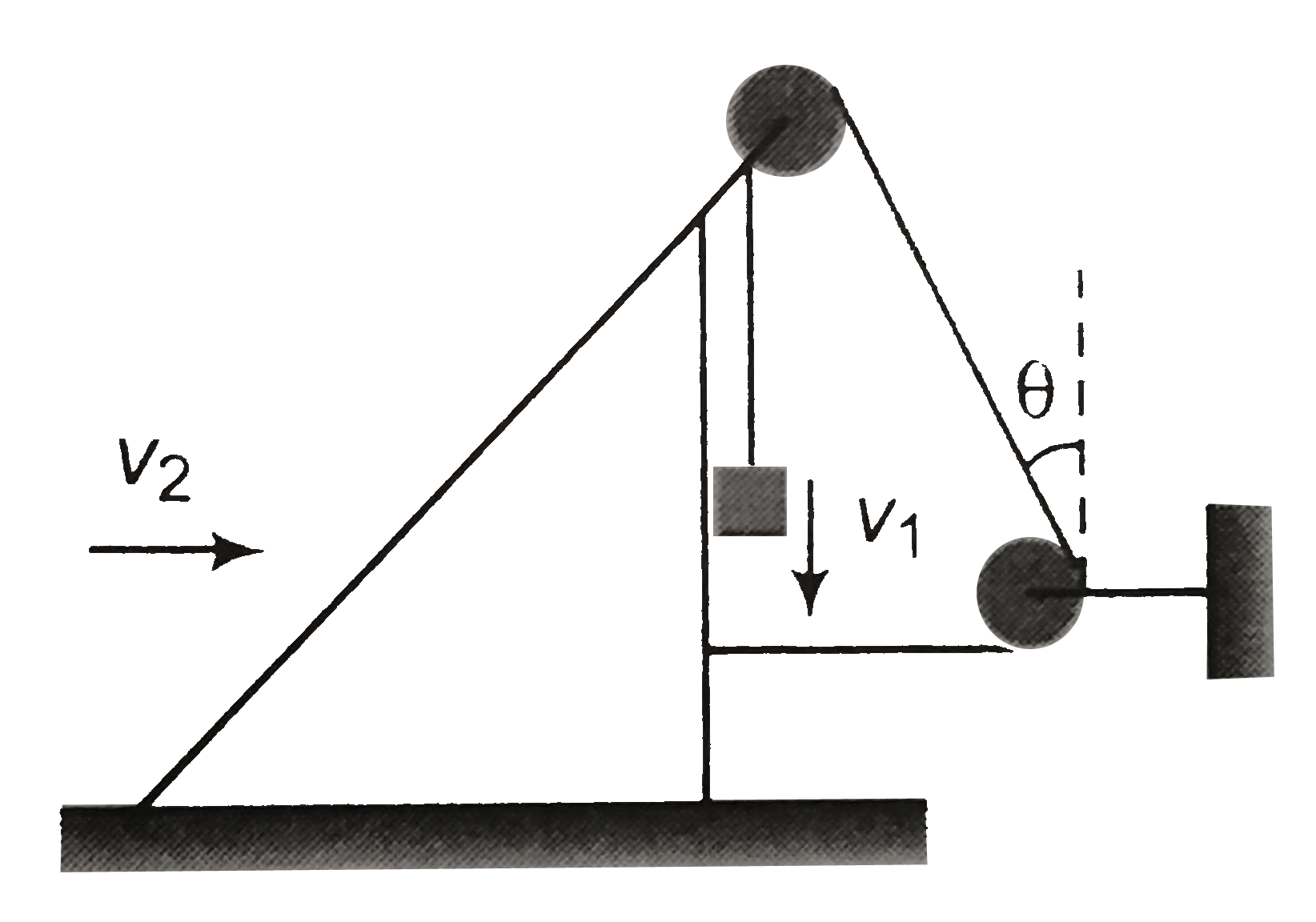
The block A is moving downward with constant velocity Find the velocity of the block B. When the string makes an angle with the horizontal
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:
Step by step video & image solution for The block A is moving downward with constant velocity v_(0.) Find the velocity of the block B. When the string makes an angle theta with the horizontal by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-2)
9 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (O-1)
50 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
Similar Questions
A ladder is hanging from ceiling as shownin figure. Three men A, B and C of masses 40 kg, 60 kg, and 50 kg are climbing the ladder. Man A is going up with retardation 2m/s2, C is going up with an acceleration of 1m/s2 and man B is going up with a constantg speed of 0.5 m/s. Find the tension in the string supporting the ledder. [g=9.8m/s2]

View SolutionA ball of mass m kept at the corner as shown in the figure, is acted by a horizontal force F. The correct free body diagram of ball is

View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionIn the figure block moves downwards with velocity v1, the wedge rightwards with velocity v2. The correct relation between v1 and v2 is
View SolutionIf block A is moving horizontally with velocity v_(A) , then find the velocity of block B at the instant as shown in fig.
View SolutionConsider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is v_(0) in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle theta with horizontal
View Solutionltbgt Find the velocity of block B when ring A is moving downward with velocity v.
View Solution
In the figure, the pulley P moves to the right with a constant speed v0. If the velocity of B is v in downward direction, find the velocity of A.
View SolutionIn the system shown, the block A is moving down eith velocity v1 and C is moving up with velocity v3. Express velocity of the block B in terms of velocities of the blocks a and C.

View SolutionBlock B shown in figure , moves downwards with a constant velocity of 20 cm//s . At t = 0, block A is moving upward with a constant acceleration, and its velocity is 3cm//s . If at t = 3s blocks C has moved 27 cm to the right, determine the velocity of block C at t = 0 and the acceleration of A and C.
View SolutionKnowing that block B starts to move downward with a constant velocity of 18cm/sec, the velocity of block A will be:
View SolutionBlock 5 shown in figure moves to the right with a constant velocity of 30 cm/s. Find :

(a) The velocity of block A.
(b) The velocity of the point P of the string.
(c) The velocity of the point M of the string.
(d) The relative velocity of the point P of the string with respect to the block A.
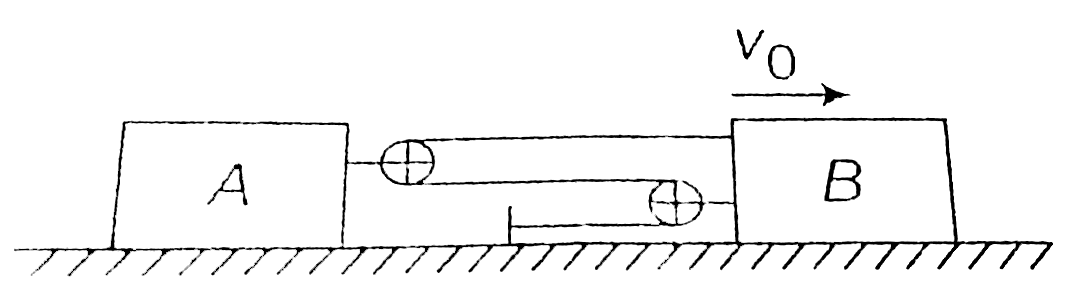
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body A relative to B is
View SolutionA smooth sledge is moving with constant velocity v0 toward left. A block is pushed toward right with a velocity v0 (relative to ground).

(A) Find the velocity with which the block escapes from the sledge and necessary critical v0 for escaping from the sledge
(B) Will the block launch onto the sledge again?
View Solution
