The sum of n terms of an A.P is 715 .If first term is increased by 1, second term is increased by 3, third term is increased by 5 and so on kth term is increased by kth odd integer then sum of n tems is 836 then value of (n6) is Solution in Gujrati
The correct Answer is:1.83
Step by step video & image solution for The sum of n terms of an A.P is 715 .If first term is increased by 1, second term is increased by 3, third term is increased by 5 and so on k^(th) term is increased by k^(th) odd integer then sum of n tems is 836 then value of (n/6) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - MATHEMATICS
34 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS SECTION-I
20 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - Chemistry
95 Videos
- SEQUENCE AND PROGRESSIONBOOK - ALLEN CHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)
10 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
136 Videos
Similar Questions
5∑k=01sin[(K+1)θ]sin[(K+2)θ] can be equal to
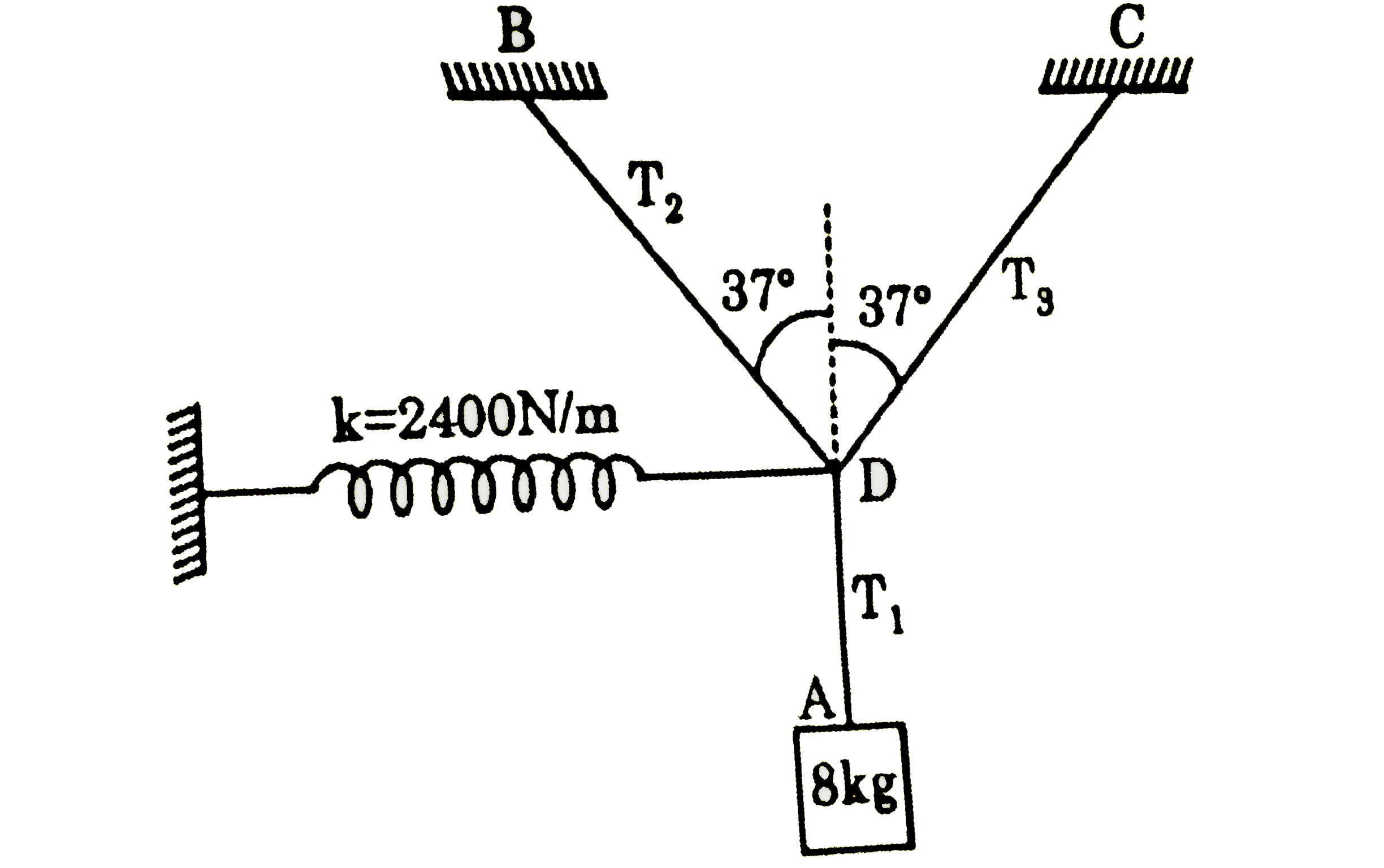
View SolutionGiven arrangement is in equilibrium and elongation in spring is 1cm. Tension in string AD is T1, in string BD is T2 and is string CD is T3.Choose correct values of T1,T2andT3:
View SolutionWhich of the following statement(s) is/are correct
View SolutionThe minimum value of the sum of real numbers a−5,a−4,3a−3,1,a8 and a10 with a>0 is
View SolutionIf a be sum of the odd numbered terms and b the sum of even numbered terms of the expansion (1+x)n,n ε N then (1−x2)n is equal to
View SolutionFind the sum to n terms of the A.P., whose kthterm is 5k+1.
View SolutionShow that the ratio of the sum of first n terms of a G.P. and the sum of (n+1)th term to (2n)th term is 1rn.
View SolutionShow that the ratio of the sum of first n terms of a G.P. to the sum of terms from (n+1)th to (2n)th term is 1rn.
View SolutionThe sum of 'n' terms of an A.P is 715.If first term is incrased by 1, second term is increased by 3, third term is increased by 5 and so on kth term is increased by kth odd integer then sum of 'n' tems is 836 then value of (n/6) is
View Solutionदिखाइए कि एक गुणोत्तर श्रेणी के प्रथम n पदों के योगफल तथा (n + 1) वें पद से (2n) वें पद तक के पदों के योगफल का अनुपात 1rn है।
View SolutionThe first term of a sequence is 12 and the second term is 14. Each term thereafter is the sum of the all the terms before it , If the nth term is the first term of the sequence that is an integer , what is the value of n ?
View SolutionIf the sum of the first nth terms of an A.P is 4n−n2 , what is the first term (that is S1) ? What is the sum of first two terms? What is the second term? Similarly, find the 3rd , the 10th and the nth terms.
View SolutionIf the nth term of an A.P is 2n−1 then sum to n terms of that A.P. is ........... .
View Solutionthe ratio of the sum of first n terms of a G.P. to the sum of terms from (n+1)th to (2n) th term is
View SolutionThe ratio of sum of m terms to the sum of n terms on an A.P is m2:n2 .If Tk is the Kth term, then T5T2 is
(A) 6
(B) 5
(C) 4
(D) 3
View SolutionShow that the ratio of the sum of first n terms of a G.P. to the sum of terms from (n+1)th to (2n)th term is 1rn .
View Solution
