[Gujrati] A circumcircle is a circle which passes through all vertices

$5 \sum k = 0 \frac{1}{sin [(K + 1) θ] sin [(K + 2) θ]}$ can be equal to

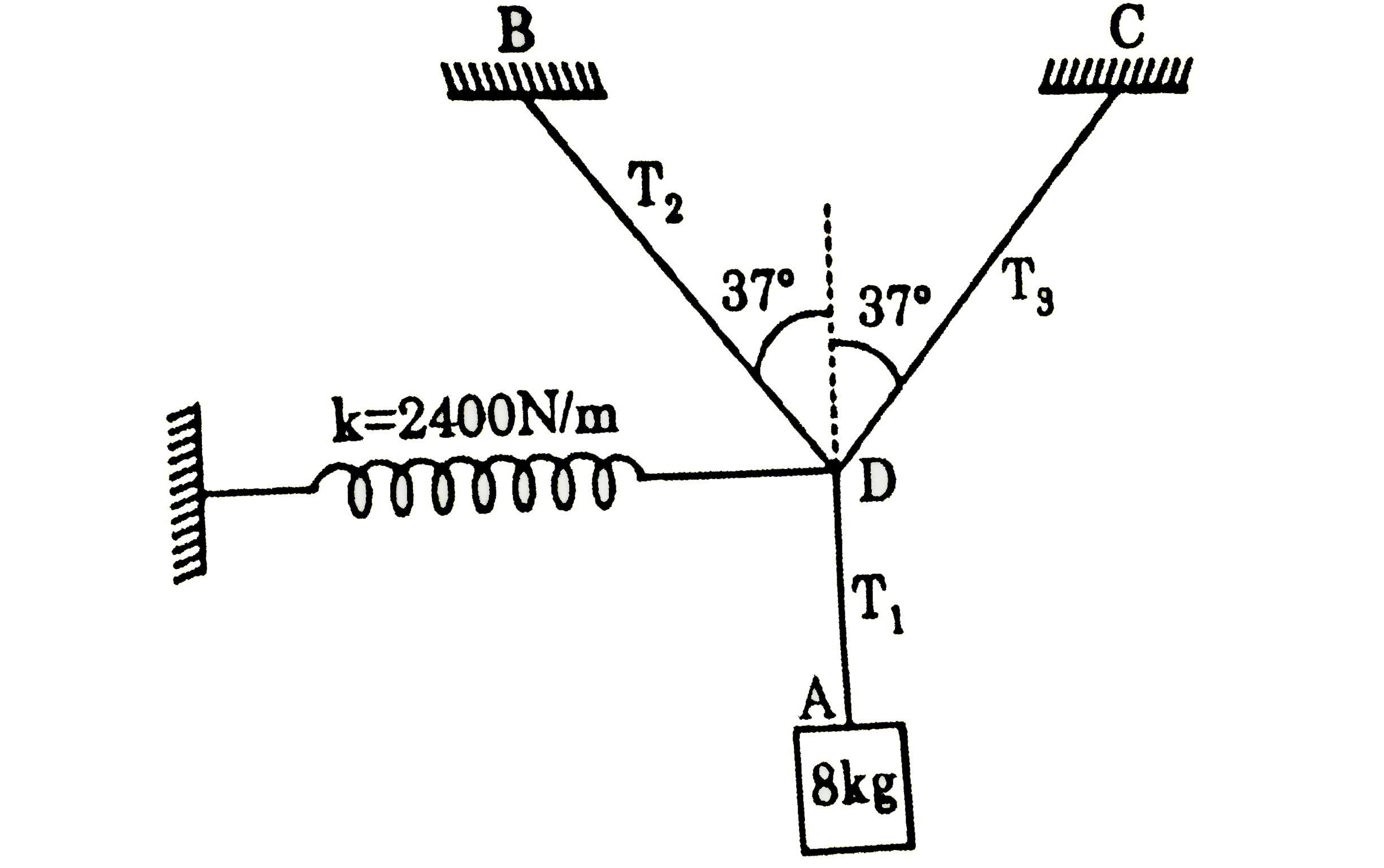
Given arrangement is in equilibrium and elongation in spring is 1cm. Tension in string AD is $T_{1}$ , in string BD is $T_{2}$ and is string CD is $T_{3}$ .Choose correct values of $T_{1}, T_{2} and T_{3}$ :
ocr_image

View Solution

Which of the following statement(s) $i s / a r e$ correct

View Solution

The minimum value of the sum of real numbers $a^{- 5}, a^{- 4}, 3 a^{- 3}, 1, a^{8} and a^{10} with a > 0$ is

View Solution

If a be sum of the odd numbered terms and b the sum of even numbered terms of the expansion ${(1 + x)}^{n}$ , $n$ $ε$ $N$ $t h e n$ ${(1 - x^{2})}^{n}$ is equal to

View Solution

In triangle $A B C, a : b : c = 4 : 5 : 6 .$ The ratio of the radius of the circumcircle to that of the incircle is____.

View Solution

Radius of incircle and circumcircle of an equilateral triangle

View Solution

A circumcircle is a circle which passes through all vertices of a triangle and an incircle is a circle which is inscribed in a triangle touching all sides of a triangle. Let ABC be a right-angled triangle whose radius of the circumcircle is 5 and its one side AB = 6. The radius of incircle of triangle ABC is r. Area of Delta ABC is

View Solution

A circumcircle is a circle which passes through all vertices of a triangle and an incircle is a circle which is inscribed in a triangle touching all sides of a triangle. Let ABC be a right angled triangle whose radius of circumcircle is 5 and its one side AB = 6. The radius of incircle of triangle ABC is r. The value of r is

View Solution

A circle having centre as O' and radius r' touches the incircle of $Δ A B C$ externally at. F, where F is on BC and also touches its circumcircle internally at G. It O is the circumcentre of $Δ A B C$ and I is its incentre, then

View Solution

In a $Δ A B C$ , if $a : b : c = 4 : 5 : 6$ , then the ratio of the radius of the circumcircle to that of the incircle is

View Solution

The radius of the circumcircle of a right angled triangle is 15 cm and the radius of its inscribed circle is 6 cm. Find the sides of the triangle.

View Solution

In $Δ A B C, ∠ A = \frac{π}{3}$ and its incircle of unit radius. Find the radius of the circle touching the sides AB, AC internally and the incircle of $Δ A B C$ externally is x , then the value of x is

View Solution

Let the centroid of an equilateral triangle ABC be at the origin. Let one of the sides of equilateral triangle be along the straight line x+y=3. If R and r be the radius of circumcircle and incircle respectively of $△ A B C$ , then (R+r) is equal to :

View Solution

In triangle $A B C, ∠ B A C = 90^{\circ}, A B = 6$ cm and BC = 10 cm. A circle is drawn inside the triangle which touches all the sides of the triangle (i.e., an incircle of $Δ A B C$ is drawn).Find the area of the triangle excluding the circle.

View Solution

A circle having centre as O' and radius r' touches the incircle of $Δ A B C$ externally at. F, where F is on BC and also touches its circumcircle internally at G. It O is the circumcentre of $Δ A B C$ and I is its incentre, then

View Solution

The correct Answer is: $2.00$

Topper's Solved these Questions

Similar Questions

ALLEN -TEST PAPER-MATHS

The correct Answer is:2.00

Topper's Solved these Questions

Similar Questions

ALLEN -TEST PAPER-MATHS

The correct Answer is: $2.00$