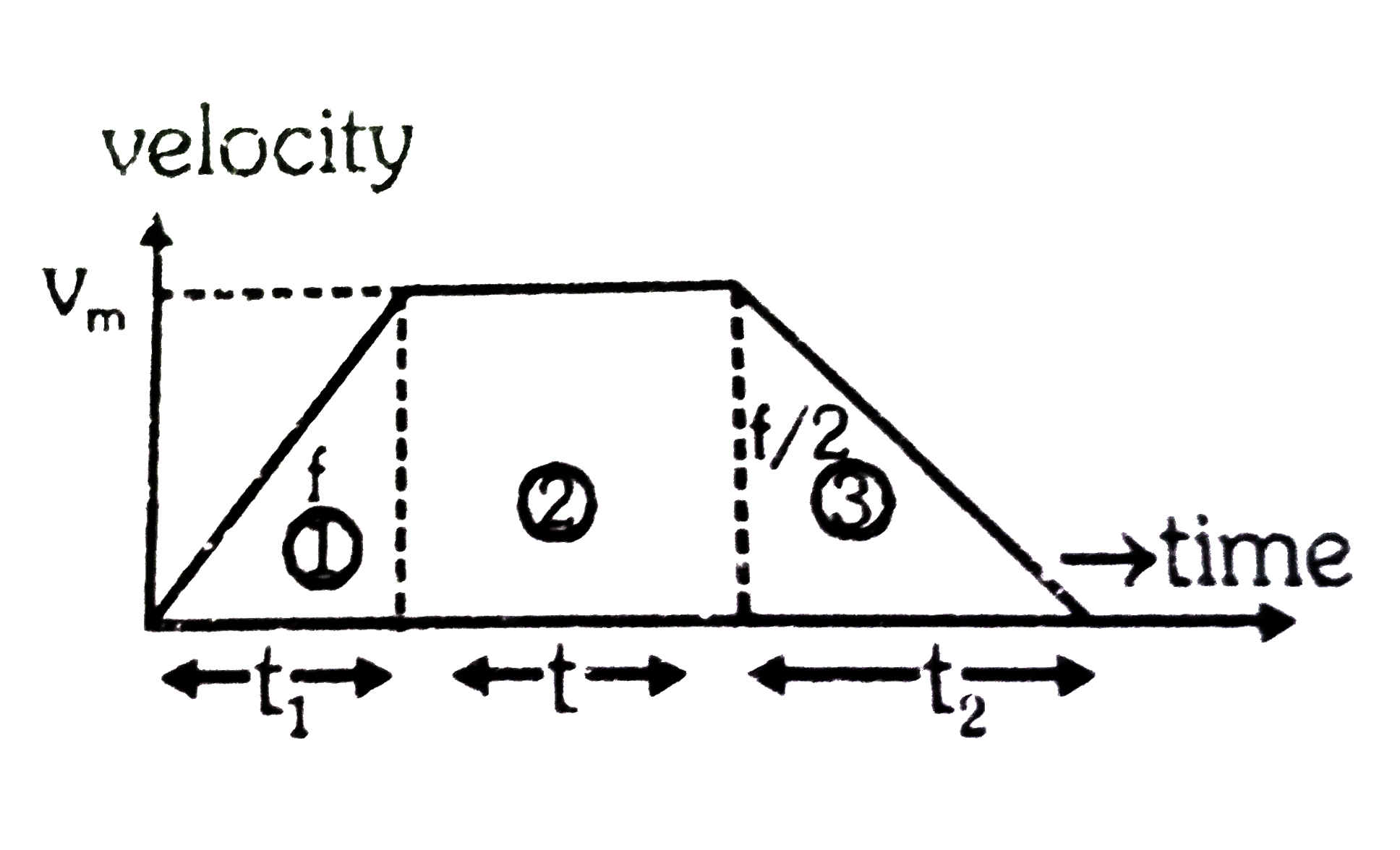
A car , starting from rest, accelerates at the rate f through a distance S then continues at constant speed for time t and then decelerates at the rate f2 to come to rest . If the total distance traversed is 15S , then Solution in Gujrati
for time t1vm=ft1 and S=12ft21
for time t30=vm−f2t2⇒t2=2t1
S3=12(f2)t22=(f4)(4t21)=ft21=2S
Therefore S+vmt+2S=15S⇒vmt=12S⇒ft1t=12S
⇒f(2Sf)1/2t=12S⇒2Sf=144S2t2⇒S=ft272
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-1
99 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-2
170 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - Integer Type Question
3 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
The distance x of a particle moving in one dimensions, under the action of a constant force is related to time t by the equation, t=√x+3, where x is in metres and t in seconds. Find the displacement of the particle when its velocity is zero.
View SolutionThe velocity of a particle moving with constant acceleration at an instant t0 is 10m/s After 5 seconds of that instant the velocity of the particle is 20m/s. The velocity at 3 second before t0 is:-
View SolutionA stone is dropped from the top of a tower of height h. Aftre 1s another stone is droppped from the balcony 20m below the top. Both reach the bottom simultaneously. What is the value of h ? Take g=10ms−2.
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA car, starting from rest, accelerates at the rate (f) through a distance (S), then continues at constant speed for some time (t) and then decelerates at the rate f/2 to come to rest. If the total distance is 5S, then prove that
S=12/ft∘.
View SolutionA car, starting from rest, accelerates at the rate f through a distance s, then continues at constant speed for time t and then decelerates at the rate f/ 2 to come to rest. If the total distance travelled is 15 s, then
View SolutionA car starts from rest and travels a distance s with a uniform acceleration f, then it travels with uniform velocity for a time t, and at last comes to rest with a uniform retardation (f)/(2) . If the total distance travelled is 5s. Then
View SolutionA car, starting from rest, accelerates at the rate f through a distance S, then continues at constant speed for time t and then decelerates at the rate f2 to come to rest. If the total distance traversed is 5 S, then :
View SolutionA car starting from rest, accelerates at a constant rate x for sometime after which it decelerates at a constant rate y to come to rest. If the total time elapsed is t, the maximum velocity attained by the car is given by
View SolutionA car starting from rest, accelerates at the rate of f through a distance S, then continues at constant speed for time t and declerates at the rate f/2 to come to rest. If the total distance travelled is 15 S then S =
View SolutionA car starting from rest,accelerates at the rate of f through a distance S,then continues at constant speed for time t and declerates at the rate f/2 to come to rest.if the total distance travelled is 15 S then S=
View SolutionA car accelerates from rest at a constant rate α for some time,after which it decelerates at a constant rate β and comes to rest .If the total time elapsed is t,then the maximum velocity acquired by the car is
View SolutionA car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β and comes to rest. If the total time elapsed is t, then the maximum velocity acquired by the car is
View SolutionA car starting from rest, accelerates at the rate of f through a distance S, then continues at constant speed for time t and declerates at the rate f//2 to come to rest. If the total distance travelled is 15 S then S =
View SolutionA car starting from rest, accelerates at the rate of f through a distance S, then continues at constant speed for time t and declerates at the rate f/2 to come to rest. If the total distance travelled is 15 S then S =
View Solution
