An electorn moves in a circle of radius 10cm with a constant speed of 4.0×106ms−1.Find the electric current at a point on the circle.Solution in Gujrati
Let the position vectors of m1 and m2 be r1 and r2.
The position vector of the center of mass, measured from the same origin, is
R=m1r1+m2r2m1+m2
where we have neglected the mass of the thin rod. The center of mass lies on the line joining m1 and m2. To show this, suppose first that the tip of R dows not lie on the line, and consider the vectors r1r2 from the tip of R to m1 and m2
 From the sketch we see that r1=r1−R
From the sketch we see that r1=r1−R
r2=r2−R
Using equation (1) gives r1=r1−m1r1m1+m2−m2r2m1+m2=m2m1+m2(r1−r2)
r2=r2−m1r1m1+m2−m2r2m1+m2=−(m1m1+m2)(r1−r2)
r1 and r2 are propotional to r1−r2, the vector from m1 to m2. Hence r1 and r2 lie along the line jpining m1 and m2 as shown.
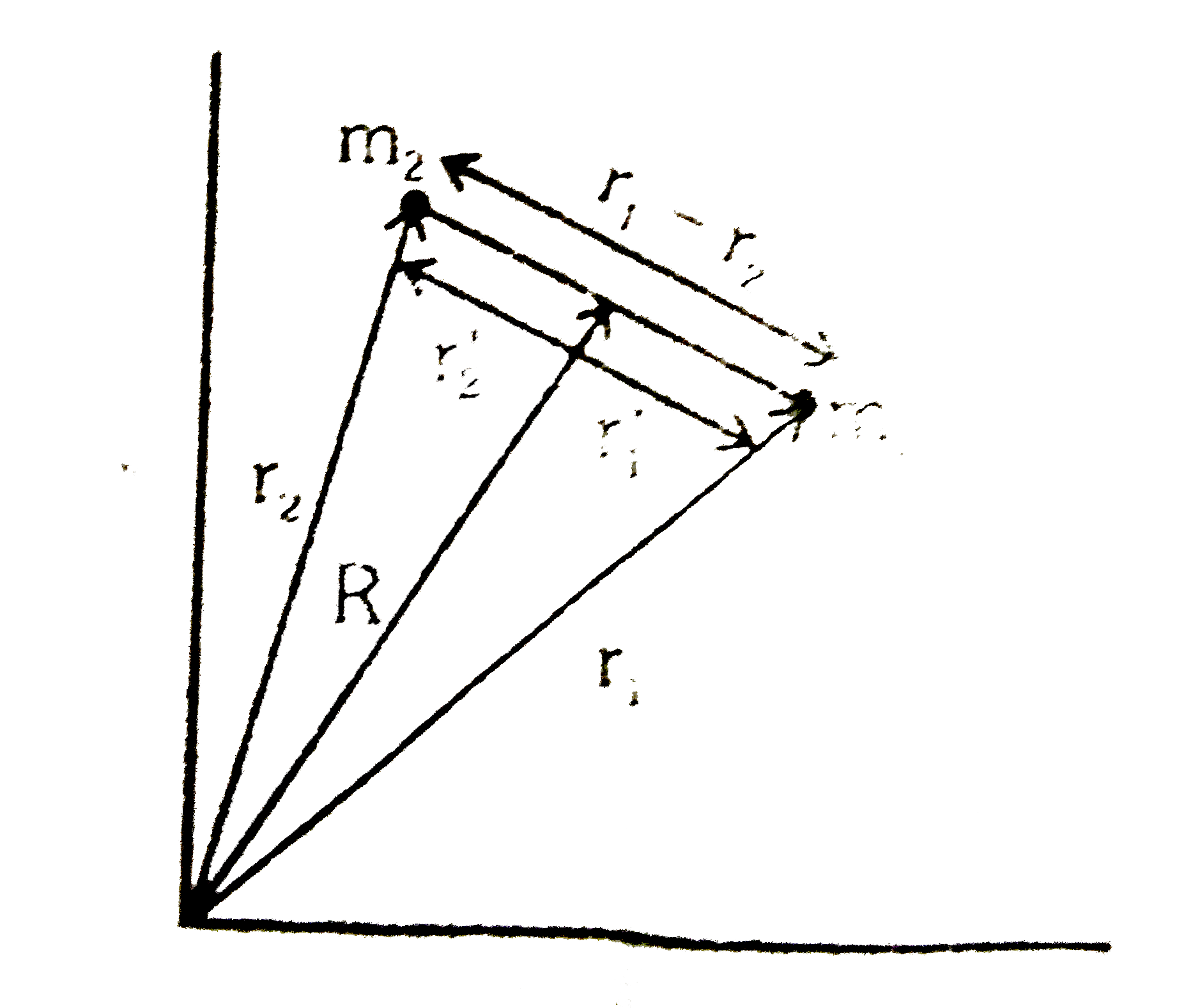
Furthermore, r1=m2m1+m2(r1−r2)=m2m1+m2
r2=m1m1+m2(r1−r2)=m1m1+m2l
Assuming that friction is negligible, the external force on the baton is F=m1g+m2g
The equation of motion of the center of mass is (m1+m2)R=(m1+m2)g or R=g
 The center of mass follows the parabolic trajectory of single mass in a uniform gravitational field.
The center of mass follows the parabolic trajectory of single mass in a uniform gravitational field.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III
26 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A
32 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
Similar Questions
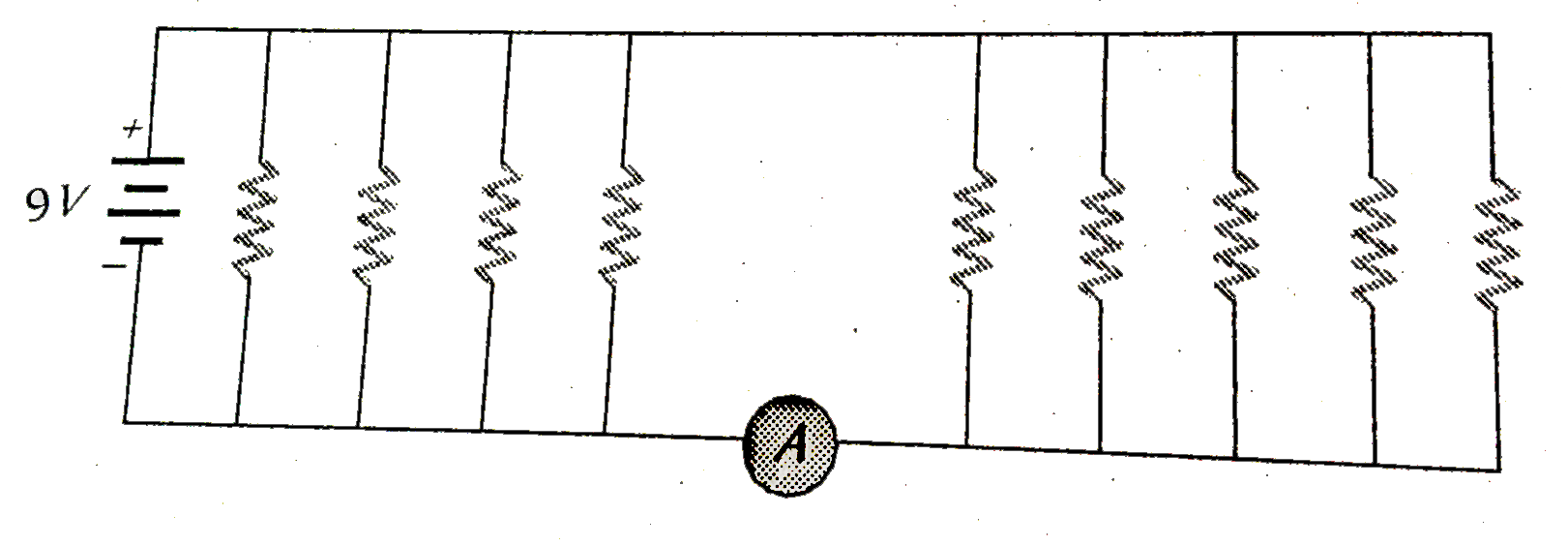
If each resistance in the figure is of 9Ω then reading of ammeter is
View SolutionBy a cell a current of 0.9 A flows through 2 ohm resistor and 0.3A through 7 ohm resistor. The internal resistance of the cell is
View SolutionA ball of mass (m)0.5kg is attached to the end of a string having length (L)0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of angular velocity of ball (radian/s) is -
 .
.
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.

(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View SolutionA point is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
View SolutionA body is moving in a circle with a speed of 1ms−1. This speed increases at a constant rate of 2ms−1 every second. Assume that the radius of the circle described is 25m. The total accleration of the body after 2s is.
View SolutionIf a body moves with a constant speed in a circle
View SolutionAn electron moves in a circle of radius pi can with uniform speed 5 xx 10^6 m//sec . Find the electric current at point on the circle. (Take pi^2 = 10 ).
View SolutionA particle is moving at uniform speed 2 ms^(-1) along a circle of radius 0.5m .The centripetal acceleration of particle is
View SolutionThe work done in maving a unit n- pole round a conductor carrying current in a circle of radius 10cm is w . The work done in moving it in a circle of radius 20cm is
View SolutionA proton moving with a velocity of 2×106ms−1 describes circle of radius R in a magnetic field. The speed of an α− particle to describe a circle of same radius in the same magnitude field is
View SolutionAn electron moves in a circular orbit of radius 10 cm with a constant speed of 4.0×106ms−1. Determine the electric current at a point on the orbit.
View SolutionFrom a point P, 10cm away from the centre of a circle, a tangent PT of length 8cm is drawn. Find the radius of the circle.
View SolutionIf a charge q is moving in a circle of radius r with speed v, then the equivalent current will be :
View SolutionA particle is moving in a circle with a constant speed. Its moving is
View SolutionA proton moving with a velocity of 2 xx 10^6 ms^-1 describes a circle of radius R in a magnetic field. The speed of an alpha -particle to describe a circle of same radius in the same magnetic field is
View Solution
