In hydrogen atom, the electron makes 6.6×1015 revolutions per second around the nucleus in an orbit of radius 0.5×10−10m. It is equivalent to a current nearly Solution in Gujrati
Making use of the result obtained in the previous example, distance OC of the mass center form the center is OC=2rsin(π4)3π4=4√2r3π Coordinates of the mass center (xc,yc) are (4r3π,4r3π)

Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III
26 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A
32 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
Similar Questions
If each resistance in the figure is of 9Ω then reading of ammeter is
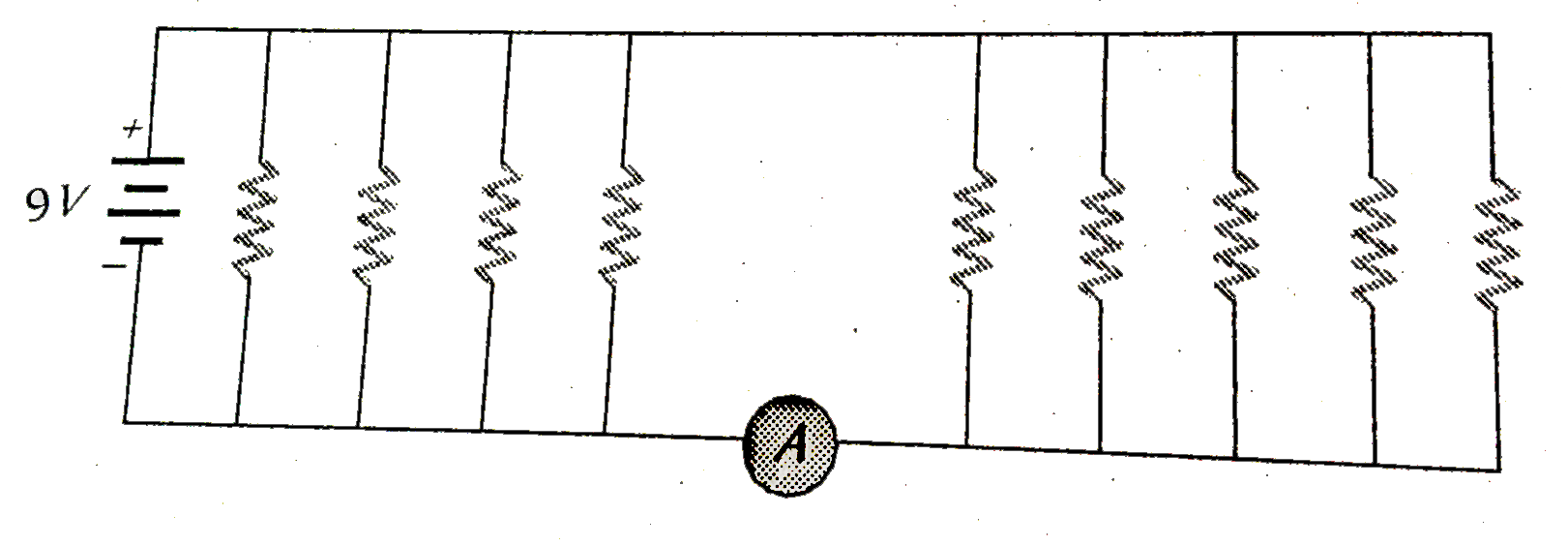
View SolutionBy a cell a current of 0.9 A flows through 2 ohm resistor and 0.3A through 7 ohm resistor. The internal resistance of the cell is
View SolutionA ball of mass (m)0.5kg is attached to the end of a string having length (L)0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of angular velocity of ball (radian/s) is -
 .
.
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.

(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View SolutionIn a hydrogen atom , the electron moves in an orbit of radius 0.5 A making 10^( 16 ) revolutions per second . The magnetic moment associtated with the orbital motion of the electron is ……
View SolutionIn an hydrogen atom, the electron revolves around the nucles in an orbit of radius 0.53 xx 10^(-10) m . Then the electrical potential produced by the nucleus at the position of the electron is
View SolutionIn Bohr model of hydrogen atom , the electron revolves around the nucleus in a circular orbit of radius 5.1 xx 10^(-11)m at a frequency of 6.8 xx 10^(15) revolutions per second. Find the equivalent current at may point on the orbit of the electron
View SolutionThe revolution of the electron in the first Bohr orbit of a hydrogen atom constitutes a current loop of area 8.8×10−21m2. If the frequency of revolution is 6.6×1015 Hz, calculate the equivalent magnetic moment and the orbital angular momentum. [y0=8.975×1010C/kg]
View Solutionहाइड्रोजन परमाणु में इलेक्ट्रॉन नाभिक के चारो और प्रति सेकंड 6.0×1015 चक्कर लगता है । कक्षा में उत्पन्न धारा का मान क्या होगा ?
View SolutionThe electon in the hydrogen atom revolves around the nucleus in an orbit of radius 0.5 A what is the equivalent magnetic moment if the frequency of revolution of the electron is 1010 MHz ?
View SolutionIn a hydrogen atom the electron is making 4×107 revolution per minute in a path of radius 0.5 A∘. Find the magnetic field produced at the centre of orbit.
View SolutionIf the electron in a Hydrogen atom makes 6.25×1015 revolutions in one second, the current is
View Solutionकिसी परमाणु में, इलेक्ट्रॉन 9.4×1018 परिक्रमण प्रति सेकण्ड बनाने वाली त्रिज्या 0.727Å के पथ के अनुदिश नाभिक के चारों ओर घूमता है। तुल्य धारा होगी
(e=1.6×10−19C)
View SolutionIn a hydrogen atom, the electron revolves round the nucleus 6.8×1015 times per second in an orbit of radius 0.53Å. What is equivalent magnetic moment ? (Given that e=1.6×10−19C).
View SolutionThe electron in a hydrogen atom circles around the positive nucleus with a speed of 2.18 xx 10^6 m//s in an orbit of radius 5.3 x 10^-11 m . Calculate the:- equivalent current
View SolutionIn an hydrogen atom, the electron revolves around the nucles in an orbit of radius 0.53×10−10m. Then the electrical potential produced by the nucleus at the position of the electron is
View Solution
