A particle is projected upwards with a velocity of 100m/s at an angle of 60∘ with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g=10m/s2.Solution in Gujrati
The correct Answer is:20 s
Step by step video & image solution for A particle is projected upwards with a velocity of 100 m//s at an angle of 60^(@) with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g = 10 m//s^(2). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
14 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-1)
40 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
A particle travels so that its acceleration is given by →a=5costˆi−3sintˆj. If the particle is located at (−3,2) at time t=0 and is moving with a velocity given by (−3ˆi+2ˆj). Find
(i) The velocity [→v=∫→a.dt] at time t and
(ii) The position vector [→r=∫→v.dt] of the particle at time t(t>0).
View SolutionA particle is projected form a horizontal plane (x−z plane) such that its velocity vector at time t is gives by →V=aˆi+(b−ct)ˆj. Its range on the horizontal plane is given by
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionA particle is projected vertically upwards with velocity 40m//s. Find the displacement and distance travelled by the particle in (a) 2s (b) 4s (c) 6s Take g=10 m//s^2
View SolutionA particle is projected vertically upwards with an initial velocity of 40 m//s. Find the displacement and distance covered by the particle in 6 s. Take g= 10 m//s^2.
View SolutionA particle A is projected with an initial velocity of 60m/s at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a)the angle of projection α of particle B, (b) time when the collision takes place and (c) the distance of P from A, where collision occurs. (g=10m/s2)

View SolutionTwo particles are projected from a tower horizontally in opposite directions with velocities 10 m//s and 20 m//s . Find the time when their velocity vectors are mutually perpendicular. Take g=10m//s^2 .
View SolutionA particle is projected at an angle 60∘ with horizontal with a speed v=20m/s. Taking g=10m/s2. Find the time after which the speed of the particle remains half of its initial speed.
View SolutionFind the maximum height reached by a particle which is thrown vertically upwards with the velocity of 20 m//s (take g= 10 m//s^(2) ).
View SolutionA particle is projected from the ground at an angle of 60∘ with horizontal at speed u=20m/s. The radius of curvature of the path of the particle, when its velocity. makes an angle of 30∘ with horizontal is :
(g=10m/s2
View SolutionA particle is projected vertically upwards from ground with velocity 10 m // s. Find the time taken by it to reach at the highest point ?
View Solutionएक कण प्रारंभिक वेग g मी/से उर्ध्वार्धर दिशा में ऊपर की और फेका जाता है। कण द्वारा तय की गई महत्तम ऊंचाई है
View SolutionA particle A is projected with an initial velocity of 60 m/s. at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50 m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a) the angle of projection ∝ of particle B,
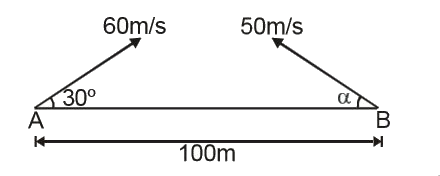
View SolutionA particle A is projected with an initial velocity of 60 m/s at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50 m/s from a A point at a distance of 100 m from A. If the particles collide in air, find (a) the angle of projection of particle B (b) timewhen the collisions takes place and (c) the distance of P from A. where collision occurs. (g=10m/s2)

View Solution
