A ball is projected on smooth inclined plane in direction perpendicular to line of greatest slope with velcoity of 8m/s. Find it's speed after 1sec.
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:10 m/s
Step by step video, text & image solution for A ball is projected on smooth inclined plane in direction perpendicular to line of greatest slope with velcoity of 8m//s. Find it's speed after 1sec. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
14 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-1)
40 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
A particle travels so that its acceleration is given by →a=5costˆi−3sintˆj. If the particle is located at (−3,2) at time t=0 and is moving with a velocity given by (−3ˆi+2ˆj). Find
(i) The velocity [→v=∫→a.dt] at time t and
(ii) The position vector [→r=∫→v.dt] of the particle at time t(t>0).
View SolutionA particle is projected form a horizontal plane (x−z plane) such that its velocity vector at time t is gives by →V=aˆi+(b−ct)ˆj. Its range on the horizontal plane is given by
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionA body is projected up with a speed v0 along the line of greatest slope of an inclined plane of angle of inclination β. If the body collides elastically perpendicular to the inclined plane, find the time after which the body passes through its point of projection.
View SolutionA body has maximum range R1 when projected up the plane. The same body when projected down the inclined plane, it has maximum range R2. Find the maximum horizontal range. Assume equal speed of projection in each case and the body is projected onto the inclined plane in the line of the greatest slope.
View SolutionA smooth ball is released from rest from a height h as shown in figure. It slides down the first inclined plane and collides with the second inclined plane. a. If e = 0 , find the speed of the ball just after leaving the inclined plane 1. b. If the particle mioves horizontally just after the collision find e .
View SolutionFind range of projectile on the inclined plane which is projected perpendicular to the incline plane with velcoity 20m/s as shwon in figure.
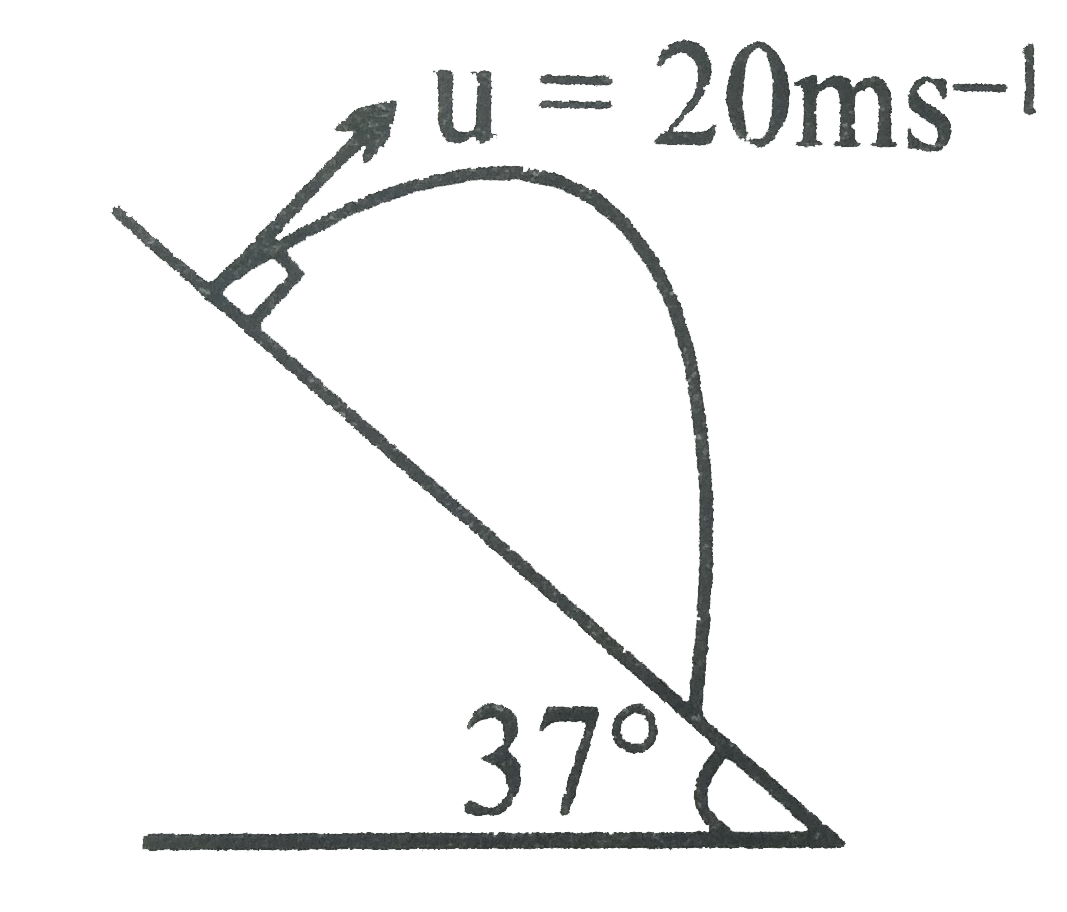
View SolutionA ball is projected perpendicularly from an inclined plane of angle theta , with speed 'u' as shown. The time after which the projectile is making angle 45^(@) with the inclined plane is :
View SolutionA small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘to the bottom edge of the slope .It returns to the edge after 2s . The ball is in contact with the inclied plane throughout the process. The angle of inclination θ is :−.
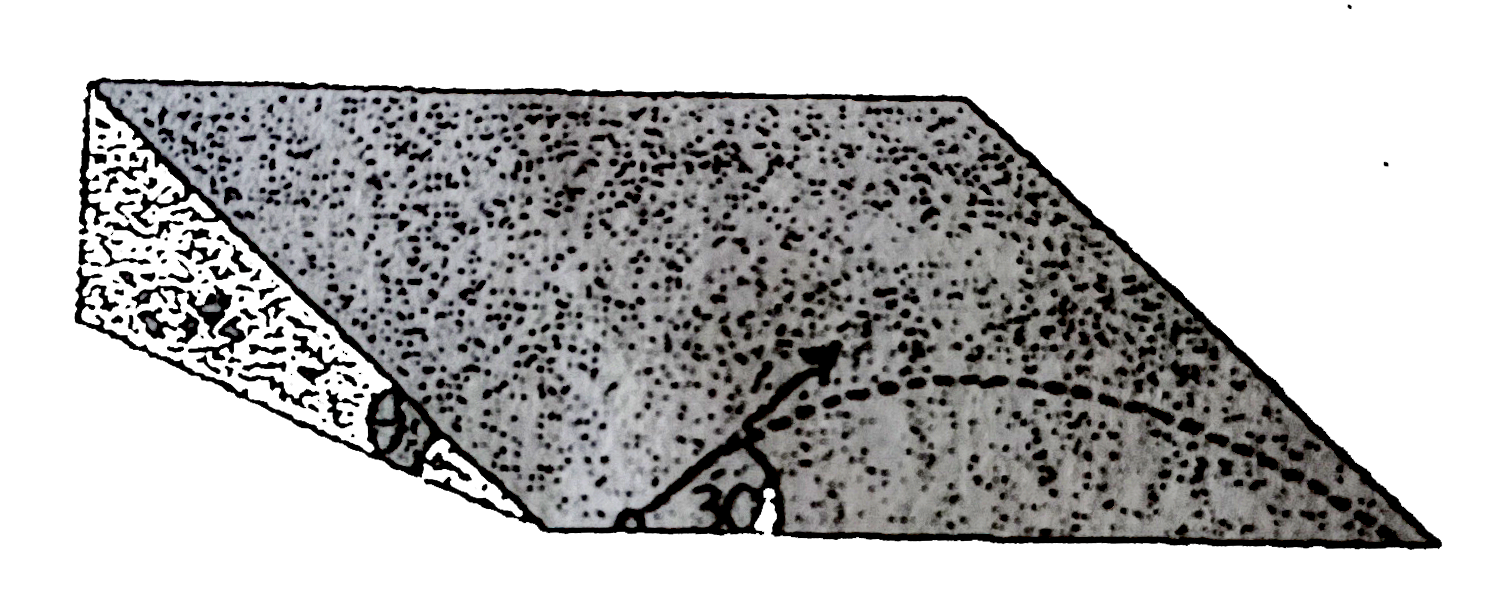
View SolutionA small ball is projected up a smooth inclined plane with an initial speed of 10 m//s along the direction at 30^(@) to the bottom edge of the slope. It returns to the edge after 2s. The ball is in constant with the inclined plane throughout the process. What is the inclination angle of the plane?
View SolutionA small ball is projected up a smooth inclined plane with an initial speed of 10m/s at 30∘ from the bottom edge of the slope. It returns to the edge after 2s. The ball is in contact with the inclined plane throughout the process. The inclination angle (in degree) of the plane is N. The value of N/6 is
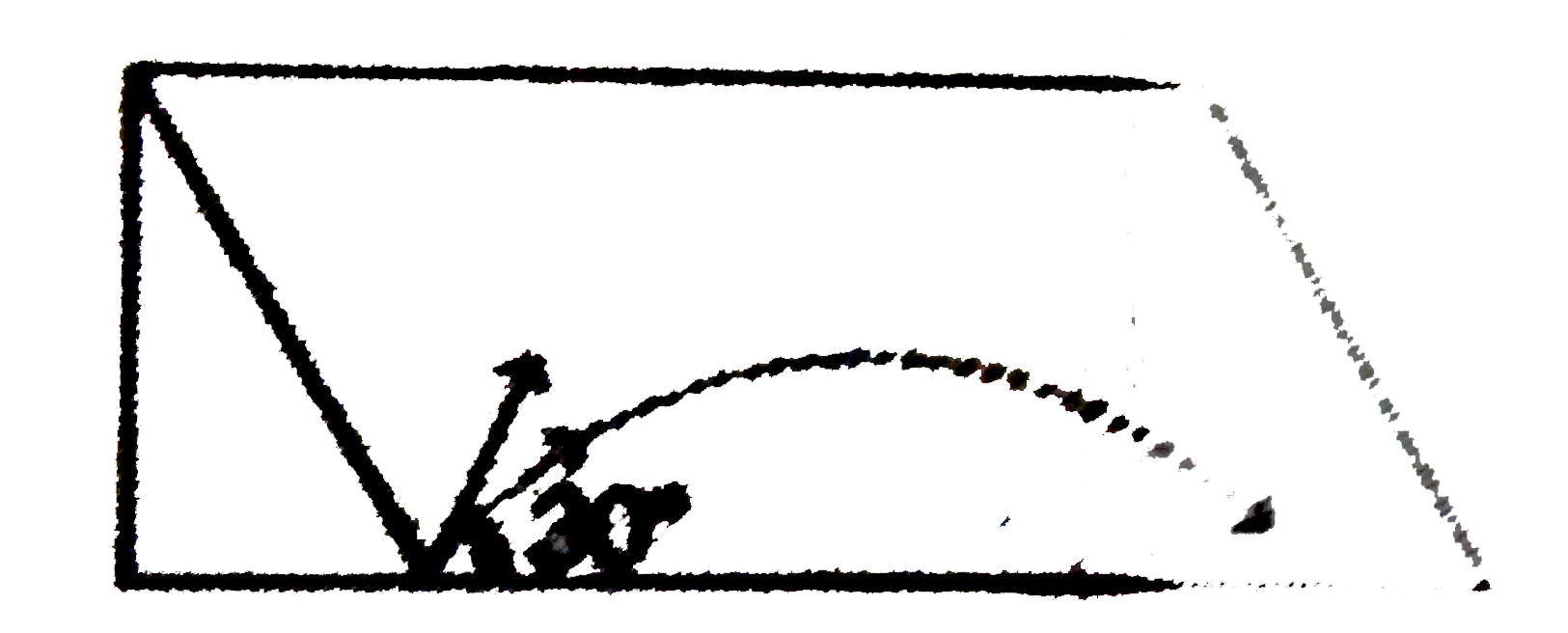
View SolutionThe line of greatest slope on an inclined plane P1 is that line in the plane which is perpendicular to the line of intersection of plane P1 and a horiontal plane P2.
Q. Assuming the plane 4x−3y+7z=0 to be horizontal, the direction cosines of line greatest slope in the plane 2x+y−5z=0 are
View SolutionThe line of greatest slope on an inclined plane P1 is the line in the plane P1 which is perpendicular to the line of intersection of the plane P1 and a horizontal planeP2.
Q. The coordinate of a point on the plane 2x+y−5z=0,2√11 unit away from the line of intersection of 2x+y−5z=0and4x−3y+7z=0 are
View SolutionA ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is

View Solution
