[Gujrati] By the term velocity of rain, we mean velocity with which ra

A particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows $u_{x} = 3 m / s, u_{y} = 4 m / s, a_{x} = 2 m / s^{2} and a_{y} = 1 m / s^{2} .$ The rate of change of speed at this moment is

View Solution

A particle travels so that its acceleration is given by $\to a = 5 cos t ˆ i - 3 sin t ˆ j$ . If the particle is located at $(- 3, 2)$ at time $t = 0$ and is moving with a velocity given by $(- 3 ˆ i + 2 ˆ j)$ . Find
(i) The velocity $[\to v = \int \to a . d t]$ at time t and
(ii) The position vector $[\to r = \int \to v . d t]$ of the particle at time $t (t > 0)$ .

View Solution

Assertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.

View Solution

A particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If $α and β$ are the base angles of triangle and angle of projection is $θ$ , then prove that $(tan θ = tan α + tan β)$

View Solution

By the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
${\to v}_{r m} = {\to v}_{r} - {\to v}_{m}$
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.
ocr_image
When you are standstill in rain, you have to hold umbrella vertically to protect yourself.
(a) When you walk with velocity 90 cm/s, you have to hold your umbrella at $53^{\circ}$ above the horizontal. What is velocity of the raindrops relative to the ground and relative to you ?
(b) If you walk with speed 160 cm/s, how should you hold your umbrella ?

View Solution

By the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
${\to v}_{r m} = {\to v}_{r} - {\to v}_{m}$
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.
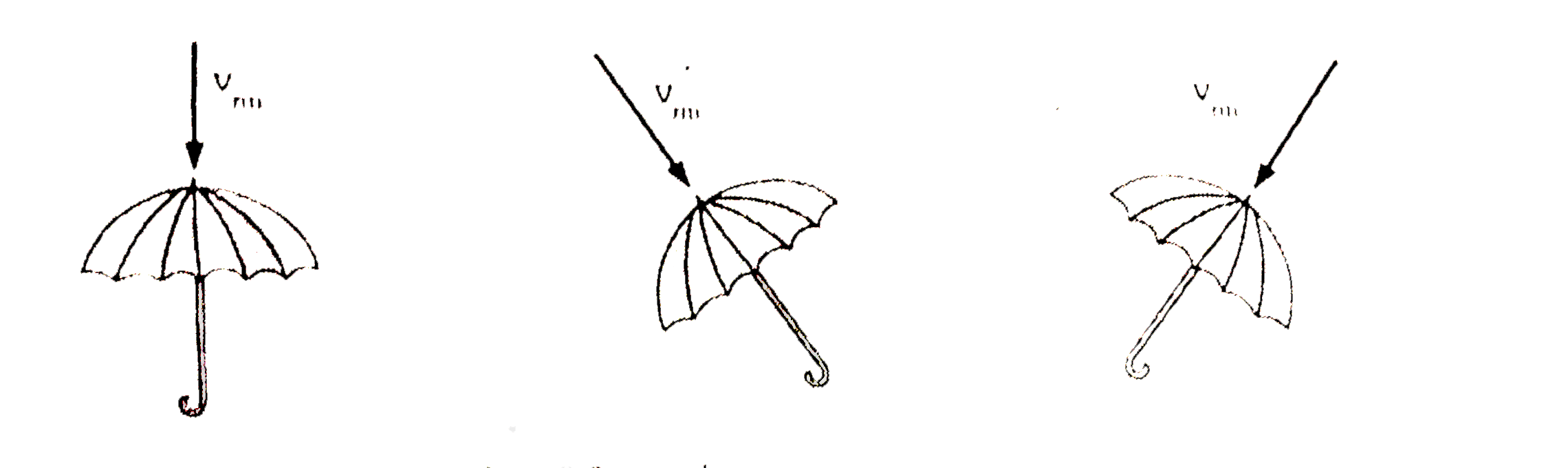
ocr_image
A man walks in rain at 72 cm/m due east and observes the rain falling vertically. When he stops, rain appears to strike his back at $37^{\circ}$ from the vertical. Find velocity of raindrops relative to the ground.

View Solution

By the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation. vec(v)_(rm)=vec(v)_(r)-vec(v)_(m) A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure. When you walk in rain at 75 cm/s, you have to hold your umbrella vertically and when you double your speed in the same direction, you have to hold your unbrella at 53^(@) above the horizontal. what is the rain velocity ?

View Solution

A man moving with a velocity of 5m//s on a horizontal road observes that raindrops fall at an angle of 45^(@) with the vertical. When he moves with a velocity of 16m//s along an inclined plane, which is inclined at 30^(@) with the horizontal , he observes raindrops falling vertically downward as shown in the figure. Find the actual velocity of the raindrops.

View Solution

Gain the marginal velocity of the falling raindrops

View Solution

A train travels due south at 30 m/s (relative to the ground) in a rain that is blown toward the south by the wind. The path of each raindrop makes an angle of 70 with the vertical, as measured by an observer stationary on the ground. An observer on the train, however, sees the drops fall perfectly vertically. Determine the speed of the raindrops relative to the ground.

View Solution

Raindrops falling due to gravity do not acquire high velocity. Define the velocity of the raindrop when unbalanced force on it is zero.

View Solution

Raindrops are falling vertically with a velocity 10 m//s . To a cyclist moving on a straight road the rain drops appear to be coming with a velocity of 20m//s . The velocity of cyclist is :-

View Solution

वर्षा की बूंदें 5m/s के वेग स ऊर्ध्वाधर नीचे की ओर गिर रही है। एक साइकिल चालक उत्तर दिशा में 10m/s के वेग से चल रहा है। बारिश की बूंदें साइकिल चालक को किस प्रकार आती हुई दिखाई देगी?

View Solution

Explain why raindrops falling under gravity do not acquire high velocity.

View Solution

Raindrops are falling vertically with a velocity $10 m / s$ . To a cyclist moving on a straight road the rain drops appear to be coming with a velocity of $20 m / s$ . The velocity of cyclist is :-

View Solution

By the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
${\to v}_{r m} = {\to v}_{r} - {\to v}_{m}$
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.
ocr_image
When you are standstill in rain, you have to hold umbrella vertically to protect yourself.
(a) When you walk with velocity 90 cm/s, you have to hold your umbrella at $53^{\circ}$ above the horizontal. What is velocity of the raindrops relative to the ground and relative to you ?
(b) If you walk with speed 160 cm/s, how should you hold your umbrella ?

View Solution

The correct Answer is:(a) Vertically (b) $53^{\circ}$ above east (c) $53^{\circ}$ above west (d) $53^{\circ}$ above north (e) $45^{\circ}$ above south

Topper's Solved these Questions

Similar Questions

ALLEN -KINEMATICS-2D-Exercise (O-1)

The correct Answer is:(a) Vertically (b) 53∘ above east (c) 53∘ above west (d) 53∘ above north (e) 45∘ above south

Topper's Solved these Questions

Similar Questions

ALLEN -KINEMATICS-2D-Exercise (O-1)

The correct Answer is:(a) Vertically (b) $53^{\circ}$ above east (c) $53^{\circ}$ above west (d) $53^{\circ}$ above north (e) $45^{\circ}$ above south