Two particle A and B projected along different directions from the same point P on the ground with the same velocity of 70 m/s in the same vertical plane. They hit the ground at the same point Q such that PQ = 480,. Then [g=9.8m/s2]Solution in Gujrati
Ratio of their times of flight is 4:5
Ratio of their maximum heights is 9:16
Ratio of their minimum speeds during flights is 4:3
The bisector of the angle between their directions of projection makes 45∘ with horizontal
The correct Answer is:B, C, D
Step by step video & image solution for Two particle A and B projected along different directions from the same point P on the ground with the same velocity of 70 m/s in the same vertical plane. They hit the ground at the same point Q such that PQ = 480,. Then [g=9.8 m//s^(2)] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
14 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
A particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionA particle travels so that its acceleration is given by →a=5costˆi−3sintˆj. If the particle is located at (−3,2) at time t=0 and is moving with a velocity given by (−3ˆi+2ˆj). Find
(i) The velocity [→v=∫→a.dt] at time t and
(ii) The position vector [→r=∫→v.dt] of the particle at time t(t>0).
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
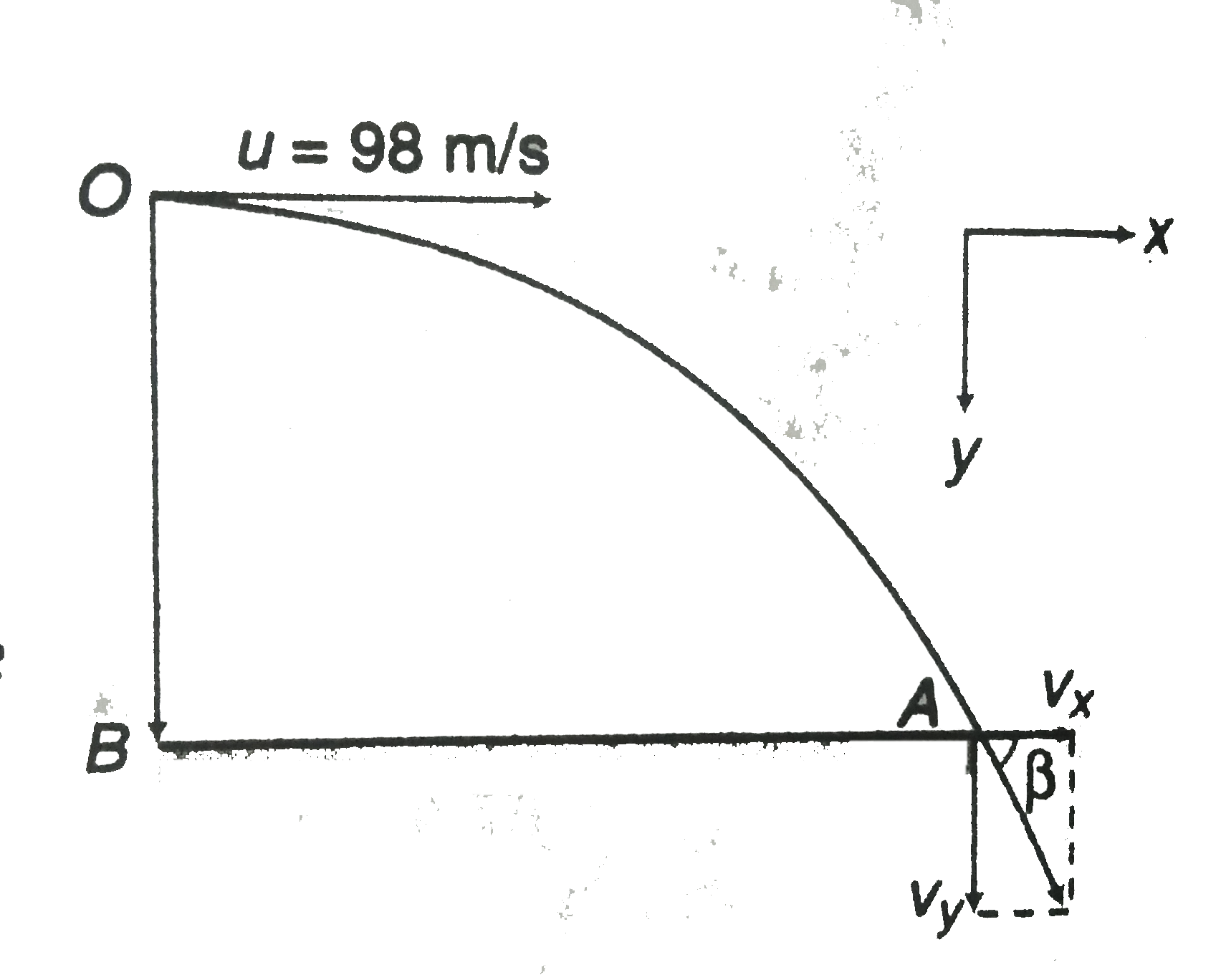
View SolutionA projectile is fired horizontally with velocity of 98 m/s from the top of a hill 490 m high. Find
(a) the time taken by the projectile to reach the ground,
(b) the distance of the point where the particle hits the ground from foot of the hill and
(c) the velocity with which the projectile hits the ground. (g=9.8m/s2)
 .
.
View SolutionTwo particles A and B are projected from the same point in different directions in such a manner that vertical components of their initial velocities are same (Fig. 5.8). Find the ratio of range. .
View SolutionTwo particles P & Q are projected simultaneously from a point O on a level ground in the same vertical plane with the same speed in directions making angle of 30∘ and 60∘ respectively with the horizontal.
View SolutionTwo particle are projected from the same point on ground simultaneously with speed 20m//s and 20//sqrt(3)m//s at angle 30^(@) and 60^(@) with the horizontal in the same direction. The maximum distance between them till both of them strikes the ground is approximately (g=10m//s^(2))
View SolutionA number of particles are projected from a given point with equal velocities in different directions in the same vertical plane. At any instant they will lie on
View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then :
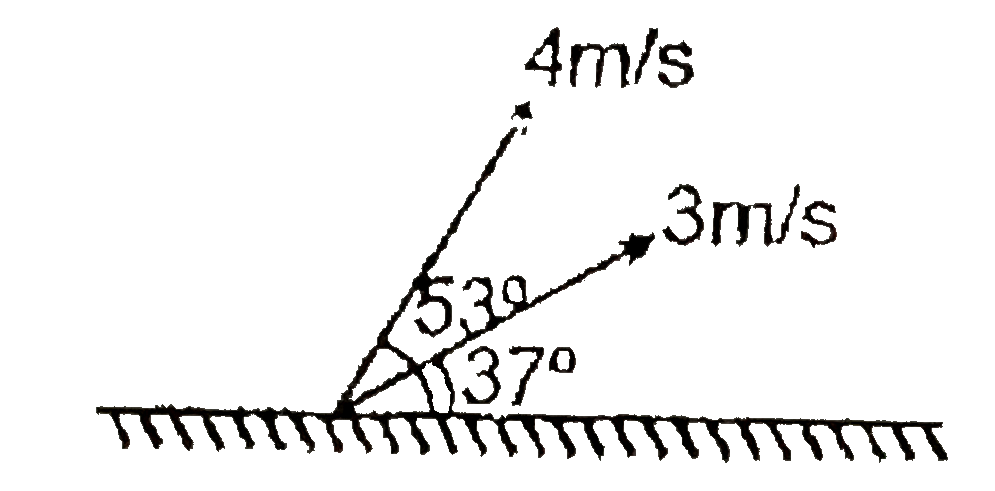
View SolutionTwo particle A and B projected along different directions from the same point P on the ground with the same velocity of 70 m/s in the same vertical plane. They hit the ground at the same point Q such that PQ = 480,. Then [g=9.8m/s2]
View SolutionTwo balls are thrown simultaneously, A vertically upwards with a speed of 20 m/s from the ground, and B vertically downwards from a height of 40 m with the same speed along the same line of motion. At what point do the two balls collide? Take g = 9.8 m//s^(2) .
View Solutionदो गेंदे साथ-साथ फेंकी गई जिसमे गेंद (A) जमीन से उर्ध्वाधर ऊपर की ओर 20 m/s वेग से और गेंद (B) उसी चाल से 40 m की ऊँचाई से ऊर्ध्वाधर नीचे की ओर, इसी गति रेखा के अनुदिश फेंकी जाती है। किस बिन्दु पर दोनों गेंदे टकराएंगी? (g=10m/s2)
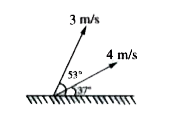
View SolutionTwo particles are projected with speed 4 m/s and 3 m/s simultaneously from same point as shown in the figure. Then:
View Solutionकिसी बिन्दु A से दो कण P एवं Q क्रमश: 15 मी/से एवं 20 मी/से के वेग से एक ही दिशा में अलग-अलग त्वरण से गुजर रहे हैं। जब P बिन्दु B पर Q के आगे बढ़ता है तो P का वेग होता है। बिन्दु B पर Q का वेग होगा
View Solutionकिसी बिन्दु A से दो कण P एवं Q क्रमशः 15 मी/से एवं 20 मी/से के वेग से एक ही दिशा में अलग - अलग त्वरण से गुजर रहे है। जब P बिन्दु B पर Q के आगे बढ़ता है तो P का वेग 30 मी/से होता है। बिन्दु B पर Q का वेग होगा
View Solution
