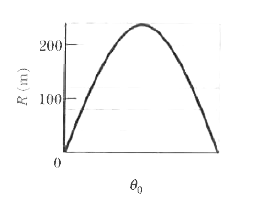
From the ground level, a ball is to be shot with a certain speed. Graph shows the range (R) of the particle versus the angle of projection from horizontal (θ).

Values of θ1 and θ2 areSolution in Gujrati
53∘ and 37∘
26.5∘ and 63.5∘
18.5∘ and 71.5∘
15∘ and 75∘
The correct Answer is:B
Step by step video & image solution for From the ground level, a ball is to be shot with a certain speed. Graph shows the range (R) of the particle versus the angle of projection from horizontal (theta). Values of theta_(1) and theta_(2) are by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A particle is projected form a horizontal plane (x−z plane) such that its velocity vector at time t is gives by →V=aˆi+(b−ct)ˆj. Its range on the horizontal plane is given by
05:32View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.04:12View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
04:11View SolutionTwo particles are projected from the same point with the same speed at different angles θ1 and θ2 to the horizontal. If their respective times of flights are T1 and T2 and horizontal ranges are same then
a) θ1+θ2=90∘ ,
b)T1=T2tanθ1
c.T1=T2tanθ2 ,
d) T1sinθ2=T2sinθ104:07View SolutionTwo particles projected at angles θ1 and θ2(<θ1) to the horizontal attain same maximum height. Which of the two particles has larger range? Find the ratio of their range.
03:45View SolutionTwo particles of equal mass 'm' are projected from the ground with speed v1 and v2 at angles θ1 and θ2 at the same times as shown in figure. The centre of mass of the two particles.
 06:20View Solution
06:20View SolutionFrom the group level, a ball is to be shot with a certain speed. Graph shows the range (R) of the particle versus the angle of projection from horizontal (θ).

Values of θ1 and θ2 are09:12View SolutionFrom the group level, a ball is to be shot with a certain speed. Graph shows the range (R) of the particle versus the angle of projection from horizontal (θ).

The corresponding time of flight vs θ graph is :-05:47View SolutionA body is projected at an angle theta with the horizontal. Derive an expression for its horizontal range. Show that there are two angles theta_(1) and theta_(2) projections for the same horizontal range, such that theta_(1)+theta_(2)=90^(@) .
View SolutionA stone projected from ground with certain speed at an angle theta with horizontal attains maximum height h_(1) when it is projected with same speed at an angle theta with vertical attains height h_(2) . The horizontal range of projectile is
04:20View SolutionA particle is projected with velocity u at angle θ1 with horizontal .The ratio of range and maximum height is 4. When it is projected at angle θ2 with horizontal with same speed,the ratio of range and maximum height is 2.Then tanθ1tanθ2 will be equal to
04:20View SolutionA ball is to be shot from level ground with a certain speed. Figure 4-38 shows the range R it will have versus the launch angle θ0. The value of θ0 determines the flight time, let tmax represent the maximum flight time. What is the least speed the ball will have during its flight if θ0 is chosen such that the flight time is 0.500tmax?
 05:23View Solution
05:23View SolutionTwo particles are projected from the same point with the same speed at different angles theta_(1) and theta_(2) to the horizontal. If their respective times of flights are T_(1) , and T_2 and horizontal ranges are same then
04:20View SolutionTwo particles are projected from the same point with the same speed at different angles θ1 and θ2 to the horizontal. If their respectively times of flights are T1 and T2 and horizontal ranges are same then
(a) θ1+θ2=90∘ (b) T1=T2tanθ1
(c) T1=T2tanθ2 (d) T1sinθ2=T2sinθ103:22View SolutionProve that, projectile from the origin theta_(0) Projection angle when projected at projection angle theta_(0)=tan^(-1)[(4H_(m))/(R)] it happens. Where H_(m) = Maximum height, R = Horizontal range
View SolutionTwo particles are projected from the same point with the same speed at different angles theta_(1) and theta_(2) to the horizontal. If their respectively times of flights are T_(1) and T_(2) and horizontal ranges are same then (a) theta_(1) + theta_(2) = 90^(@) (b) T_(1) = T_(2) tan theta_(1) (c) T_(1) = T_(2) tan theta_(2) (d) T_(1) sin theta_(2) = T_(2) sin theta_(1)
03:27View Solution

