The mass m of a body moving with a velocity v is given by m=m0√1−v2c2 where m0 = rest mass of body =10kg and c = speed of light =3×108m/s. Find the value of m at v=3×107m/sSolution in Gujrati
m=m0(1−v2c2)−1/2=10⎡⎣1−(3×1073×108)2⎤⎦−1/2=10[1−1100]−1/2≈10[1−(−12)(1100)]=10+10200≈10.05 kg
Topper's Solved these Questions
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - BEGINNER S BOX 1
2 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - BEGINNER S BOX 2
3 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
Similar Questions
Find the values of :
tan(−30∘)
View SolutionDistance between two points (8,-4) and (0,a) is 10. All the values are in the same unit of length. Find the possitive value of a.
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionA body of mass m_(1) moving with a velocity 3 m//s collides with another body at rest of m_(2) . After collision the velocities of the two bodies are 2 m//s and 5 m//s , respectively , along the direction of motion of m_(1) . The ratio m_(1)//m_(2) is
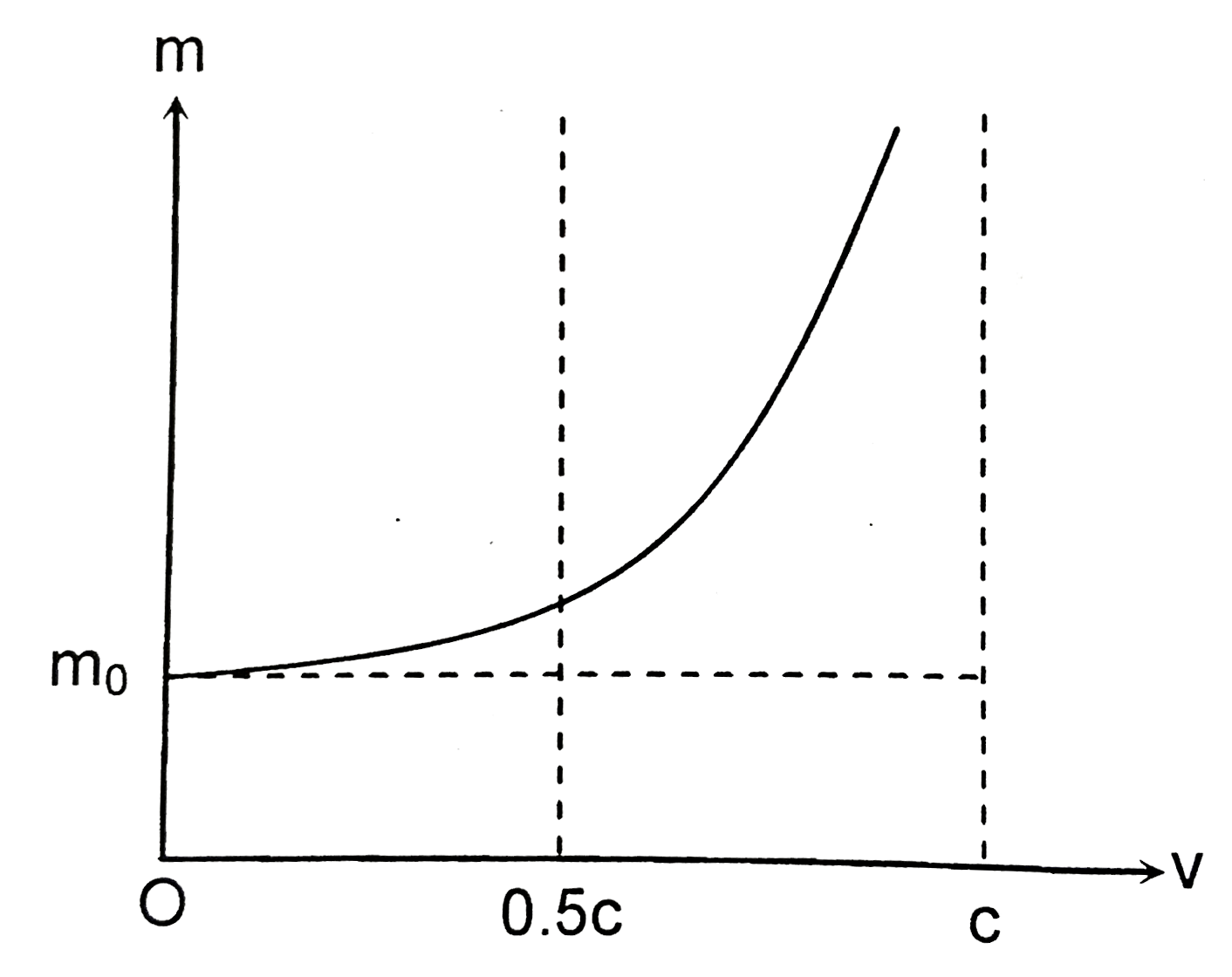
View SolutionMass m=m0√1−v2c2 as a function of a velocity is shown in the graph. m0 is the rest mass of the system. The kinetic energy of system is given as K=mc2−mcC2
Choose correct option (s)
View SolutionA body of mass m, moving along the positive x direction is subjected to a resistive force F=Kv2 (where K is a constant and v the particle n velocity). If m=10kgv=10m/s at t=0, and K=2N(m/s)−2 the velocity when t=2s is:
View SolutionA body of mass m moving with a velocity v strikes a statioinalry body of mass m and sticks to it. What is the speed of the system?
View SolutionIfv=c, the mass of the moving body, of rest mass 'm0' is _________________.
View SolutionA body of mass m _ 1 moving with an unknown velocity of v _ 1 hati , undergoes a collinear collision with a body of mass m _ 2 moving with a velocity v _ 2 hati . After collision m _ 1 and m _ 2 move with velocities of v _ 3 hati and v _ 4 hati , respectively. If m _ 2 = 0.5 m _ 1 and v _ 3 = 0.5 v _ 1 , then v _ 1 is v _ 4 - (v _ 2 ) / (x ) , where x is _________.
View SolutionA boy recalls the relation for relativistic mass (m) in terms of rest mass (m_(0)) velocity of particle V, but forgets to put the constant c (velocity of light). He writes m=(m_(0))/((1-v^(2))^(1//2)) correct the equation by putting the missing ‘c’.
View SolutionA : If m and me are moving mass, rest mass of a body and c is velocity of light, then kinetic energy of the body is E=(m−m0)c2
R : Total energy of a body is sum of kinetic energy and rest mass energy.
View SolutionA boy recalls the relation for relativistic mass (m) in terms of rest mass (m0) velocity of particle v, but forgets to put the constant c (velocity of light). He writes m= m0(1−v2)1/2 correct the equation by putting the missing 'c'.
View SolutionThe velocity v of mass m of a rocket at time t is given by the equation :
mdvdt+Vdmdt=0,
where 'V' is the constant velocity of emission. If the rocket starts from rest when t=0 with mass m, prove that :
v=Vlog(m0m).
View Solutionm1 द्रव्यमान एक एक पिण्ड 40 मी / से के एकm2 समान वेग से एक द्रव्यमान वाले स्थिर पिण्ड से टकराता है। इसके पश्चात दोनों पिण्ड एकसाथ 30 मी/से की अचर चाल से चलते है। इनके द्रव्यमानो की निष्पत्ति(m1/m2) होगी
View Solutionएक वस्तु के द्रव्यमान m को समीकरण m=m0√1−v2c2 द्वारा व्यक्त किया गया है जहां m0= वस्तु का विराम द्रव्यमान =10kg तथा c= प्रकाश का वेग =3×108m/s तो v=3×107 m/s पर m का सन्निकाट मान ज्ञात करो।
View SolutionA body of mass M moves with velocity v and collides elasticity with another body of mass m(M>>m) at rest , then the velocity of the body of mass m is
View Solution
