A particle moves on straight line according to the velocity-time graph shown in fig. Calculate -
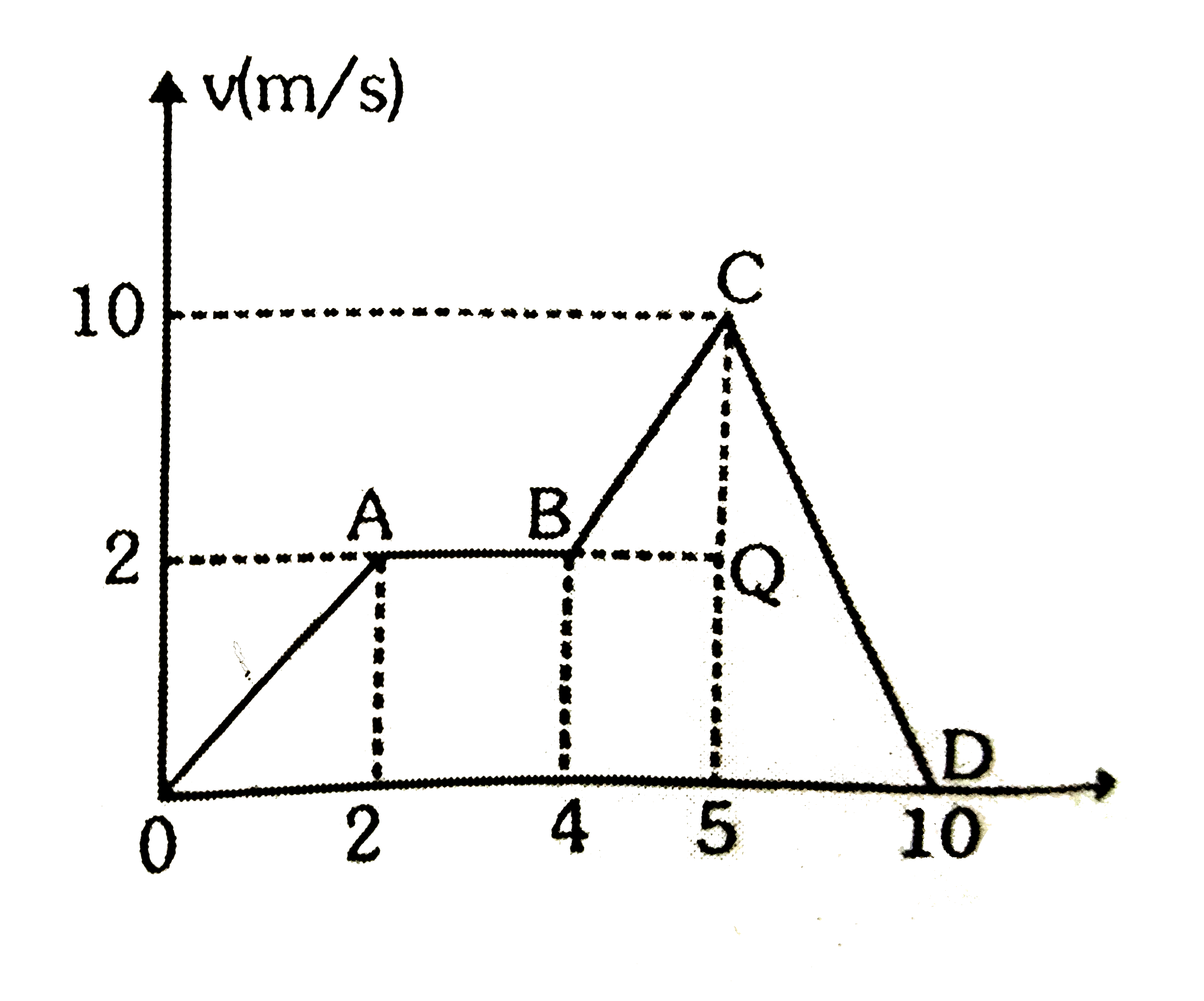
(i) Total distance covered
(ii) Average speed
(iii) In which part of the graph the acceleration is maximum and also find its value.
(iv) Retardation Solution in Gujrati
(i) Total distance covered = Area under v - t curve
=12(2×2)+2(4−2)+12(10+2)×1
12×5×10=37 m
(ii) Average speed = Total distanceTotal time=3710=3.7m/s
(iii) Acceleration = Slope of v-t curve
So maximum acceleration will be in the part where the slope will be maximum i.e. BC
amax=aBC=10−21=8m/s2
(iv) Retardation = Slope of CD (As it is negative)
=∣∣∣0−105∣∣∣=|−2|=2m/s2
Topper's Solved these Questions
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-6
9 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-4
6 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-2
89 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Question
1 Videos
Similar Questions
A particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionA particle starts from the rest, moves with constant acceleration for 15s. If it covers s1 distance in first 5s then distance s2 in next 10s, then find the relation between s1&s2.
View SolutionA student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
Based on this data, the best guess for the value of n is :-
View SolutionA simple pendulum of length l and bob mass m is hanging in front of a large nonconducting sheet having surface charge density σ. If suddenly a charge +q is given to the bob & it is released from the position shown in figure. Find the maximum angle through which the string is deflected from vertical .
 .
.
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity? .
View SolutionThe speed time graph of a body is as shown in Figure. Calculate
(i) acceleration of body, (ii) retardation of body, (iii) total distance travelled by the body.
View SolutionA particle moves in straight line. Acceleration of particle changes with velocity as showns in graph:
View SolutionPosition-time graph of a particle in motion is shown in fig. Calculate - (i) Total distance covered (ii) Displacement (iii) Average speed (iv) Average velocity.
View Solutionसरल रेखा में गति करते हुए एक कण का त्वरण समय ग्राफ चित्र में प्रदर्शित है। कण का वेग समय ग्राफ प्रापत कीजिए, यदि t=0 पर v=0 है।
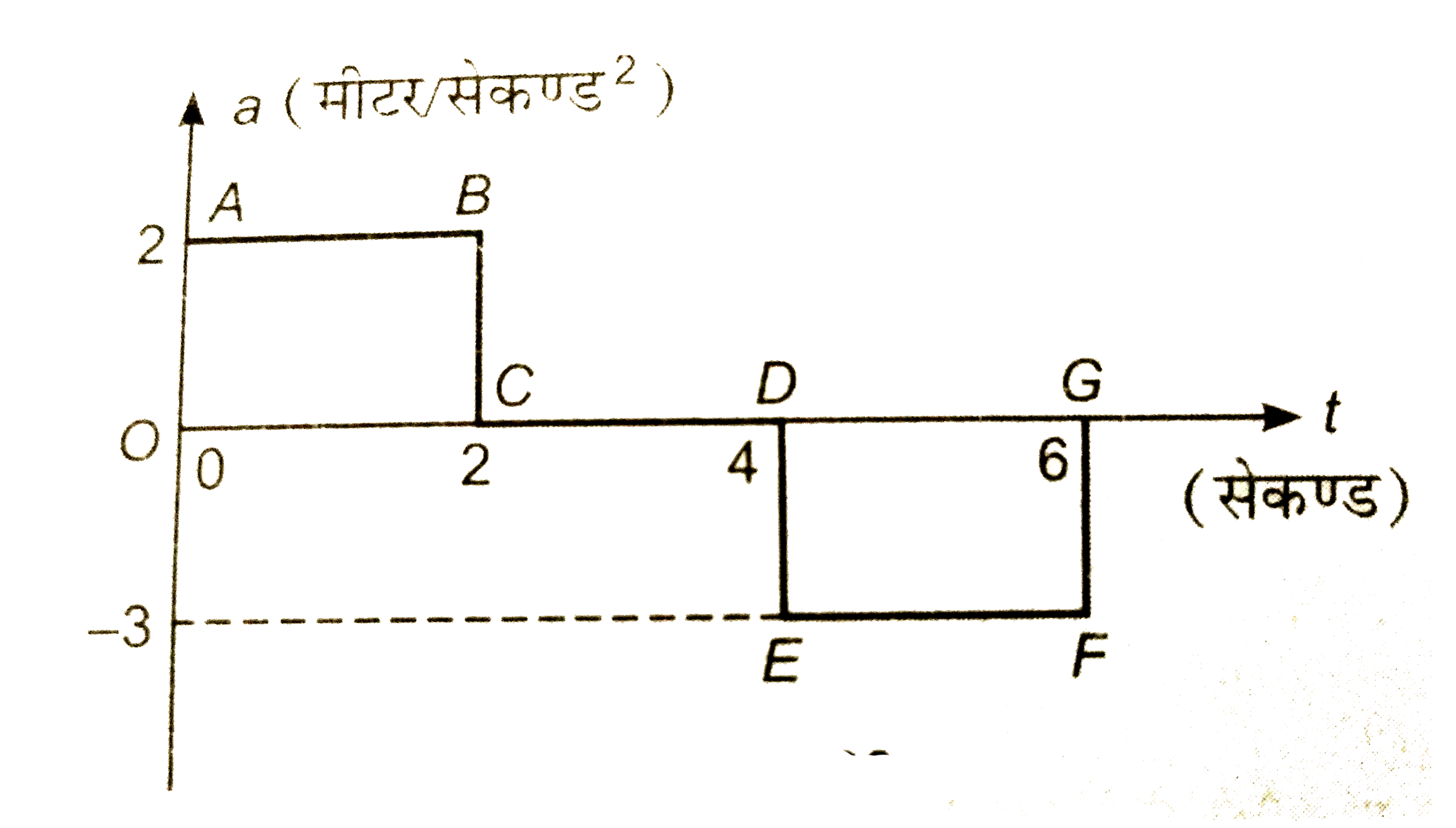
View Solutionएक सरल रेखीय गति करने वाले कण का वेग-समय ग्राफ चित्र में प्रदर्शित है| इस ग्राफ से ज्ञात कीजिए-
(i) वह समयांतराल जिसमे कण की गति एकसमान गति है|
(ii) भाग OA में त्वरण|
(iii) भाग AB में मंदन|
(iv) पहले 2 सेकंड में कण द्वारा तय किया गया विस्थापन|
View SolutionA particle is moving on a straight line such that square of its velocity is directly proportional to distance as shown in graph. What is the acceleration of the particle ?
View SolutionThe position-time graph displayed in the diagram shows the speed of the particle for which - (i) total distance covered (ii) total displacement (iii) average (iv) average
View SolutionA particle moves in a straight line according to the velocity-time graph displayed in the picture. (i) Total distance covered (ii) average (iii) In which part of the graph is the particle's acceleration maximum? Also find its value. (iv) Mandan
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
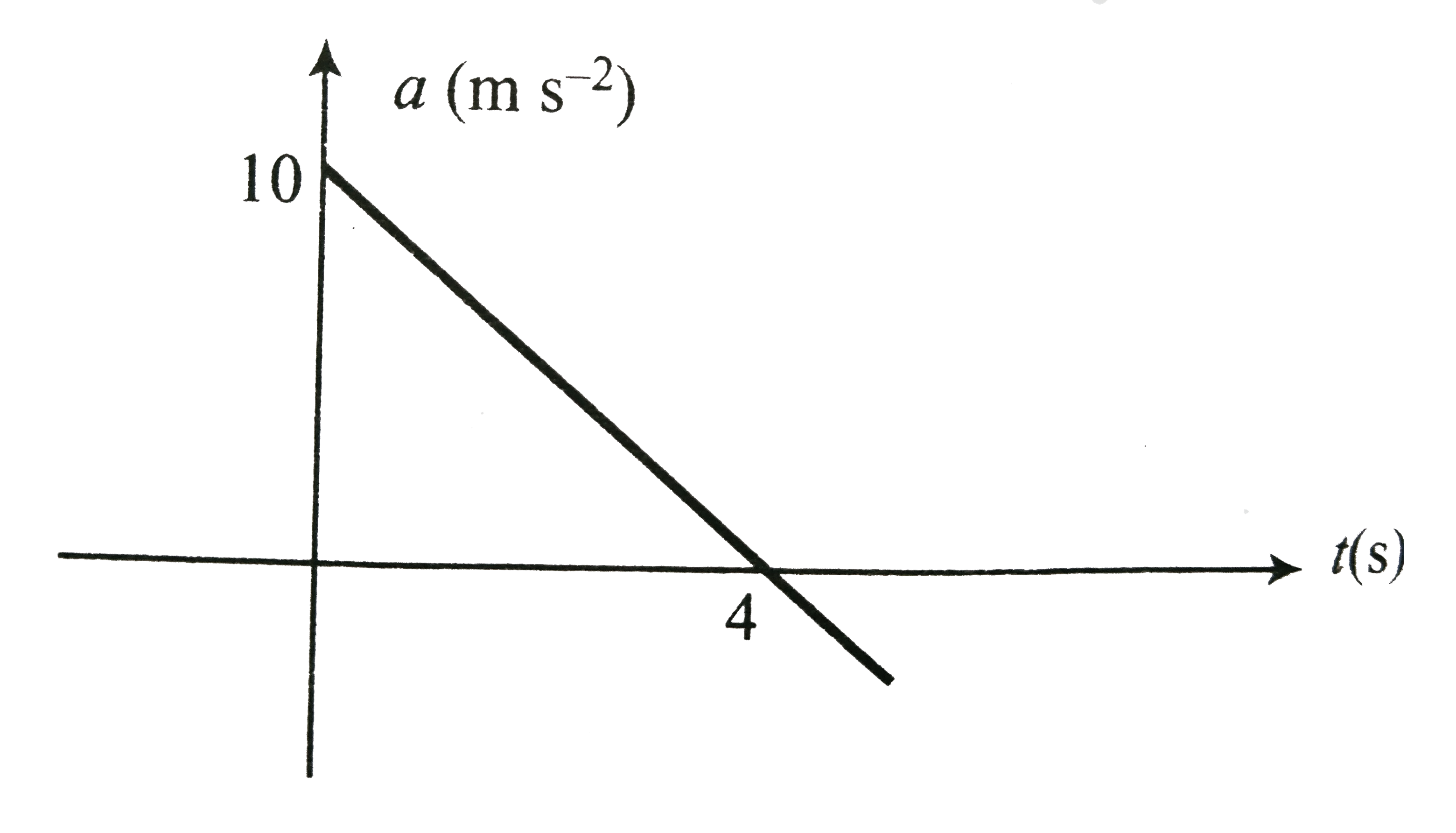 .
.
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
 .
.
View Solution
