A ball is thrown at angle θ and another ball is thrown at angle (90∘−θ) with the horizontal direction from the same point with velocity 40ms−1. The second ball reaches 50m higher than the first ball. Find their individual heights. g=10ms−2. Solution in Gujrati
For the first ball, angle of projection =θ, velocity of projection, u=40m/s.
Let h be the maximum height attained by it.
As maximum height attained = u2sin2θ2g
∴h(40)2sin2θ2×10 ...(1)
For second ball, Angle of projection =(90∘−θ).
velocity of projection, u=40m/s
Maximum height reached =(h+50) m
∴h+50=u2sin2(90∘−θ)2g=(40)2cos2θ2×10.......(2)
By adding (1) and (2),
2h+50=(40)22×10×(sin2θ+cos2θ)=(40)22×10=80
⇒2h=80−50=30⇒h=15m
Height of the first ball, h = 15m & Height of the
second ball = h+50=15+50=65m
Topper's Solved these Questions
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-6
9 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-2
89 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Question
1 Videos
Similar Questions
A particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionA student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
Based on this data, the best guess for the value of n is :-
View SolutionA simple pendulum of length l and bob mass m is hanging in front of a large nonconducting sheet having surface charge density σ. If suddenly a charge +q is given to the bob & it is released from the position shown in figure. Find the maximum angle through which the string is deflected from vertical .
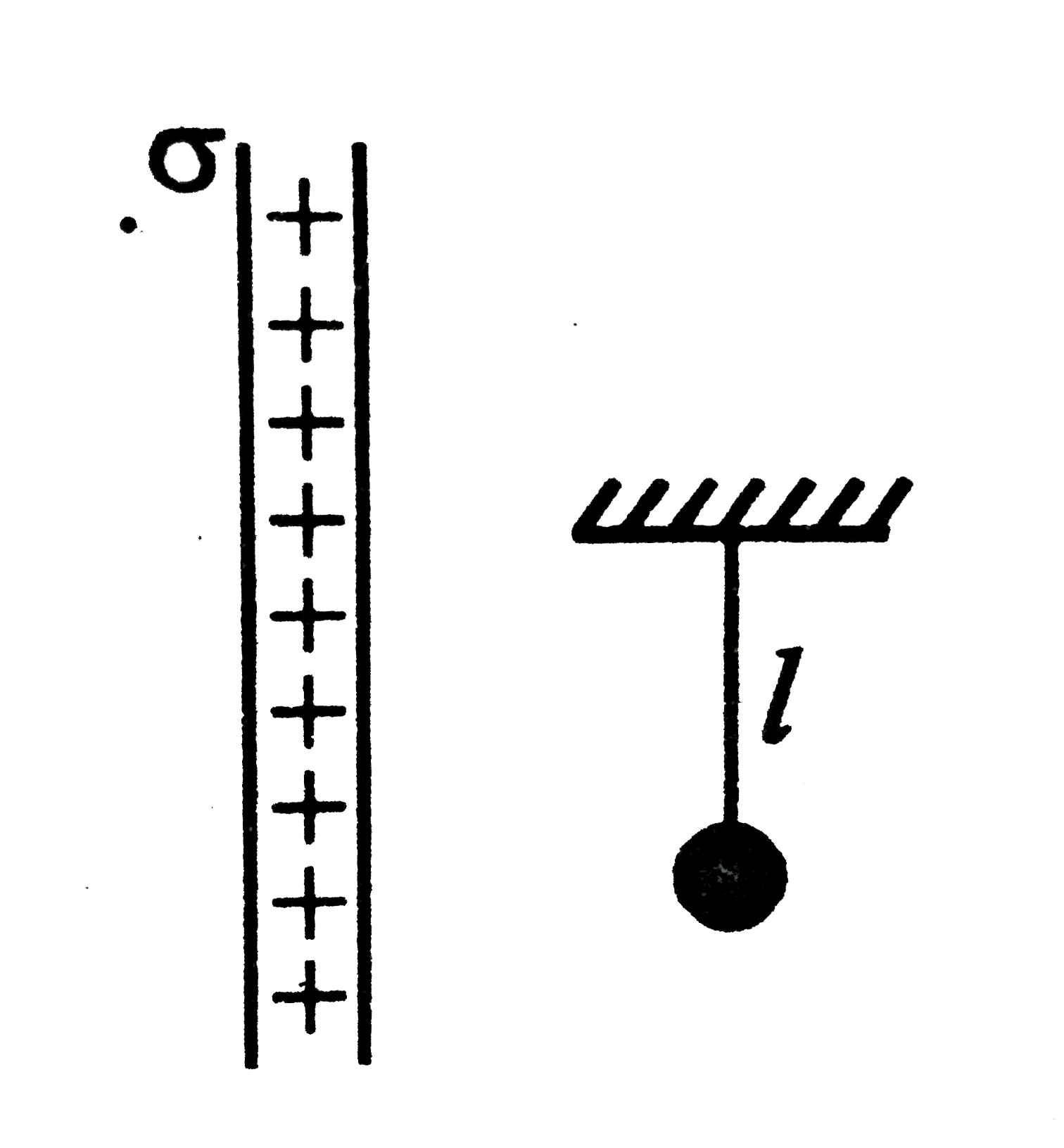 .
.
View SolutionOne body is thrown at an angke theta with the horizontal and another similar body is thrown at an angle theta with the vertical direction from the same point with same velocity 40 ms^(-1) . The second body reaches 50 metrea higher than the first body. Deteramine their individual heights. Take g= 10 ms^(-2) .
View SolutionA ball is thrown at an angle theta and another ball is thrown at an angle (90^@- tehta) with the horizontal direction from the same point, each with velocity 40 ms^(-1) . The second ball reaches 40 m higher than the first ball. Find their individul heithts, Take g= 10 m//s .
View SolutionA cricketer of height 2.5m thrown a ball at an angle of 30∘ with the horizontal such that it is received by another crickerter of same height standing at distance of 50m from the first one.Find the maximum height attained by the ball.
View SolutionIf a ball is thrown vertically upwards with a velocity of 40m/s, then velocity of the ball after 2s will be (g=10m/s2)
View SolutionA ball is thrown at angle θ and another ball is thrown at an angle (90∘−θ) with the horizontal direction from the same point with velocity 39.2ms−1. The second ball reaches 50 m higher than the first ball. Find their individual heights. Take g=9.8ms−2.
View SolutionA ball is thown at angle θ and another ball is thrown at angle (90∘−θ) with the horizontal direction from the same point each with speeds of 40 m/s. The second ball reaches 50 m higher than the first ball. Find the individual heights. g=10m/s2
View Solutionएक ही स्थान से दो गेंदे क्षैतिज से क्रमशः θ व् (90∘−θ) कोण पर 39.2 मीटर/सेकण्ड वेग से फेंकी जाती है यदि इनके द्वारा प्राप्त ऊंचाइयोँ का अंतर 50 मीटर हो तो प्रत्येक गेंद द्वारा प्राप्त अधिकतम ऊंचाई ज्ञात कीजिय । ( g=9.8 मीटर/सेकण्ड2 )
View SolutionA ball is thrown at a speed of 20 m/s at an angle of 30∘ with the horizontal . The maximum height reached by the ball is
(Use g=10m/s2)
View SolutionA ball is dropped downward from the roof of a building and simultaneously another ball is thrown in a horizontal direction, when will the balls reach the ground?
View SolutionA ball is dropped downward from the roof of a building and simultaneously another ball is thrown in a horizontal direction, when will the balls reach the ground?
View SolutionTwo balls A and B are thrown from the same point with similar velocity of 19.6ms , at angle θ and 90∘−θ with the horizontal , respectively . Ball B reaches 10 m higher than ball A. Find the individual maximum higher reached by ball A and B .
View SolutionA ball of mass 160 g is thrown up at an angle of 60^(@) to the horizontal at a speed of 10ms^(-1) . The angular momentum of the ball at highest point of the trajectory with respect to the point from which the ball is thrown is nearly (g=10ms^(2))
View SolutionA ball of mass 160 g is thrown up at an angle of 60∘ to the horizontal at a speed of 10ms−1. The angular momentum of the ball at the highest point of the trajectory with respect to the point from which the ball is thrown is nearly (g=10ms−2)
View Solution
