The 10kg collar A slides with negligible friction on the fixed vertical shaft. When the collar is released from rest at the bottom position shown, it moves up the shaft under the action of the contant force F=200N applied to the cable. The position of the small pulley at B is fixed. The spring constant k (in kilo-newton/m) which the spring must have if its maximum compression is to be limited to 0.4m is:
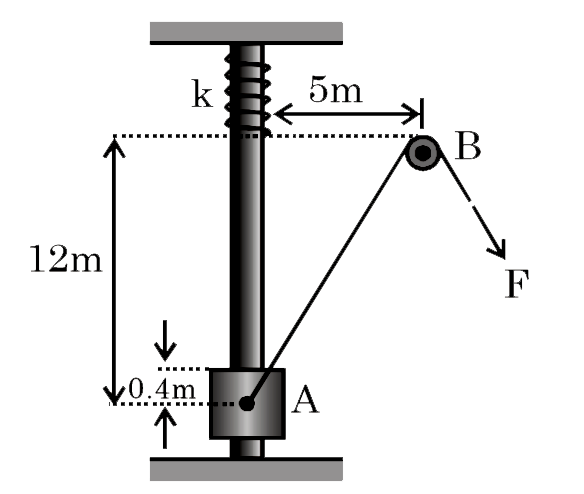 Solution in Gujrati
Solution in Gujrati
Step by step video & image solution for The 10kg collar A slides with negligible friction on the fixed vertical shaft. When the collar is released from rest at the bottom position shown, it moves up the shaft under the action of the contant force F=200N applied to the cable. The position of the small pulley at B is fixed. The spring constant k (in kilo-newton/m) which the spring must have if its maximum compression is to be limited to 0.4m is: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - CHEMISTRY
162 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
136 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - part-2 Mathematics
48 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - CHEMISTRY SECTION-II
16 Videos
- VECTOR ALGEBRABOOK - ALLEN CHAPTER - VECTOR ALGEBRAEXERCISE - All Questions
1 Videos
Similar Questions
Equal masses of three different gases X,Y,Z are mixed in a sealed rigid container. If the temperature of the system remains constant which of the following statements about the partial pressure of gas X is correct
View SolutionIf a be sum of the odd numbered terms and b the sum of even numbered terms of the expansion (1+x)n,n ε N then (1−x2)n is equal to
View SolutionP1=x+y+z+1=0,P2=x−y+2z+1=0,P3=3x+y+4z+7=0 be three planes. Find the distance of line of intersection of planes P1=0 and P2=0 from the plane P3=0.
View SolutionThe molar mass of a substance , each molecule of which contains 9 C atoms , 13 H-atoms and 3.32×10−23 g of other component is (NA=6.022×1023)
View SolutionFind the value of a, for which point P(a3,2) is the midpoint of the line segment joining the points Q(−5,4)andR(−1,0).
View SolutionThe collar A is free to slide along the smooth shaft B mounted in the frame. The plane of the frame is the vertical . Determine the horizontal acceleration a of the frame necessary to maintain the collar in a fixed position on the shaft. (g=9.8m/s2)

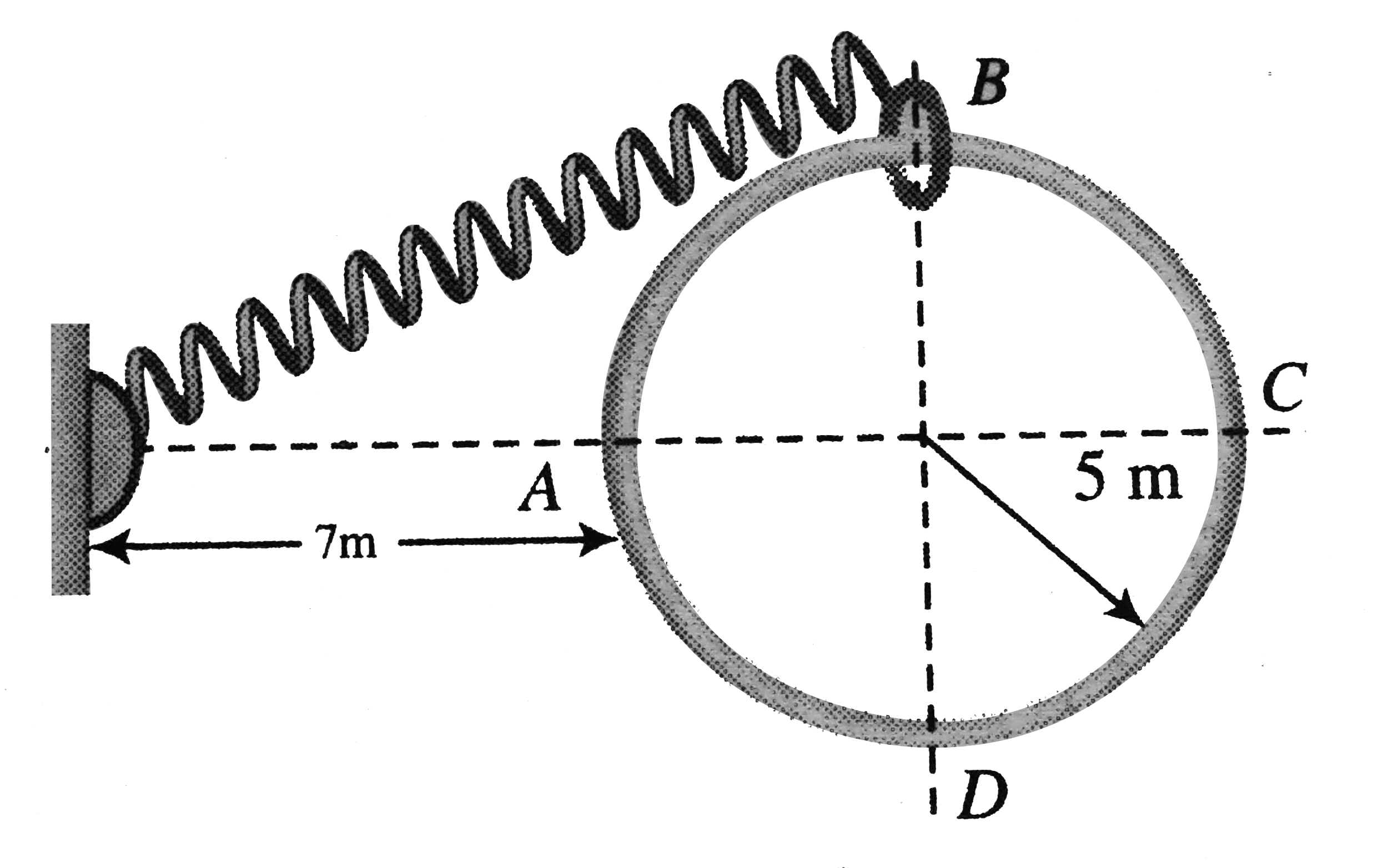
View SolutionA collar B of mass 2kg is constrained to move along a horizontal smooth and fixed circular track of radius 5m. The spring lying in the plane of the circular track and having spring constant 200Nm−1 is underformed when the collar is at A. If the collar starts from rest at B, the normal reaction exerted by the track on the collar when it passes through A is
View SolutionA 10 kg collar P slides with negligible friction on the fixed vertical shaft. When the collar is released from rest at the bottom position shown, it moves up the shaft under the action of the constant force F = 200 N applied to the cable. The position of the small pulley at B is fixed. Find the spring constant k (in k−N/m) which the spring must have if its maximum compression is to be limited to 0.4 m.

View SolutionA 2.5 kg collar attached to a spring of foce constant 1000 Nm−1 slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.
View SolutionA 10 kg collar is attached to a spring (spring constant 600 N/m.), it slides without friction over a horizontal rod. The collar iis displaced from the equilibrium position by 20 cm and released. What is the speed of the oscillation ?
View SolutionA 5 kg collar is attached to a spring of spring constant 500 N m−1. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10.0 cm and released. Calculate
(a) the period of oscillation,
(b) the maximum speed and
(c) maximum acceleration of the collar.
View SolutionA 5 kg collar is attached to a spring of spring constant 500 N m−1. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10.0 cm and released. Calculate
(a) the period of oscillation,
(b) the maximum speed and
(c) maximum acceleration of the collar.
View SolutionA 5 kg collar is attached to a spring of spring constant 500 N m−1. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10.0 cm and released. Calculate
(a) the period of oscillation,
(b) the maximum speed and
(c) maximum acceleration of the collar.
View SolutionA 5 kg collar is attached to a spring of spring constant 500 Nm^(-1) . It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. Calculate (a) The period of oscillations (b) The maximum speed and (c) maximum acceleration of the collar.
View SolutionA 5kg collar is attached to a spring of spring constant 500 Nm^(-1) . It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10.0 cm and released. Calculate the period of oscillation.
View SolutionA 5 kg collar is attached to a spring of spring constant 500 N m−1. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10.0 cm and released. Calculate
(a) the period of oscillation,
(b) the maximum speed and
(c) maximum acceleration of the collar.
View Solution
