Figure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.
Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
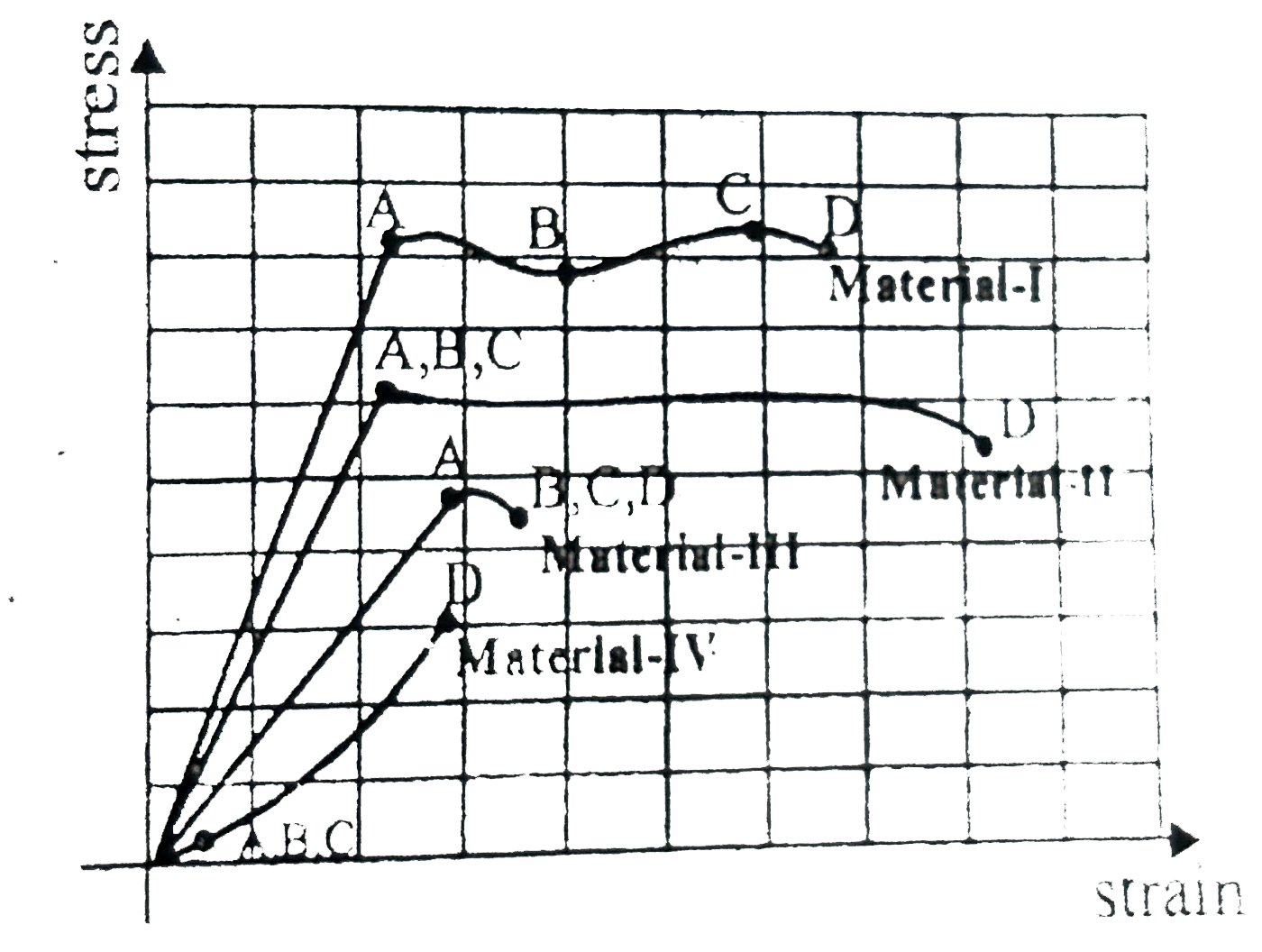
Material which is good for making wires by stretching is Solution in Gujrati
Material-I
Material-II
Material-III
Material-IIV
Step by step video & image solution for Figure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law. Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials. Material which is good for making wires by stretching is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Trigonometry)22videos
RACE
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Differentiation)40videos
RACE
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Race 215videos
RACE
- BOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
Similar Questions
Convert the angle from degree to radian :
(a) 30∘(b) 45∘(c) 60∘(d) 90∘(e) 120∘(f) 135∘(g) 210∘(h) 270∘(i) 315∘01:51View SolutionFor a straight line y=43x−4. Choose correct alternate(s)
04:45View SolutionTwo projectiles are projected with velocity vA,vB at angles θA (from horizontal) and θB (from vertical) as shown in the figure below, such that vA>vB but having same horizontal component of velocity. Which of the following is correct ?
02:42View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.01:49View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
02:12View SolutionOn gradual loading , stress - strain relationship for a metal wire is as follows . Within proportionality limit , stress prop strain or, Stressstrain = a constant for the material of wire.
Just on crossing the yield region, the material will have
02:14View SolutionAccording to Hooke's law, within the elastic limit stress/strain = constant. This constant depends on the type of strain or the type of force acting. Tensile stress might result in compressional or elongative strain, however, a tangential stress can only cause a shearing strain. After crossing the elastic limit, the material undergoes elongation and beyond a stage beaks. All modulus of elasticity are basically constants for the materials under stress.
If stress/strain is x in elastic region and y in the region of yield, then01:55View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law. Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials. Material which is good for making wires by stretching is
02:32View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law. Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials. Material which is most brittle is
03:57View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.
Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is03:59View SolutionFigure 9.11 shown the strain - stress curve for a given material. What are (a) Young's modulus and (b) approximate yield strength for this material ?
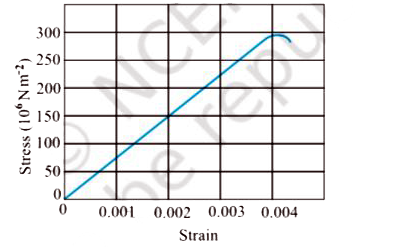05:14View SolutionFigure 9.11 shown the strain - stress curve for a given material. What are (a) Young's modulus and (b) approximate yield strength for this material ?
03:08View SolutionFigure shows the strain-stress curve for a given material. What are (a) Young's modulus and (b) approximate yield strength for this material ?
04:52View SolutionFigure show the stress-strain curve for a given material. What are (a) Young's modulus and (b) approximate yield strength of the material?
05:01View SolutionOn gradual loading , stress - strain relationship for a metal wire is as follows . Within proportionality limit , stress prop strain or, "Stress"/"strain" = a constant for the material of wire. Just on crossing the yield region, the material will have
05:48View SolutionOn gradual loading , stress - strain relationship for a metal wire is as follows . Within proportionality limit , stress prop strain or, "Stress"/"strain" = a constant for the material of wire. If "Stress"/"Strain" is x in elastic region and y in the region of yield , then
02:49View Solution